The Delboeuf, Ponzo and More Illusions

The Ebbinghaus Illusion

The Ebbinghaus illusion is a famous illusion named for its discoverer, German psychologist Hermann Ebbinghaus. He likely introduced this illusion in the 1890s, though he did not publish it in any specific publication. As shown in the figure on the right, in this illusion two circles of identical size are placed in the middle and one is surrounded by the larger circles while the other is surrounded by the smaller circles; the central circle with 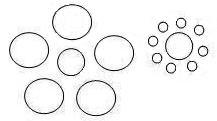larger surrounding objects appears smaller than the one with smaller objects around it. As mentioned earlier, the main explanation of the Ebbinghaus illusion is the size contrast or visual angle contrast theory, which is that the perceived size of an object is influenced by its contrast with nearby contextual objects. If the objects in the nearby surrounding context are smaller in contrast, the viewed object is perceived as larger than those without the context; and if the objects in the nearby surroundings are bigger in contrast, the object is perceived as smaller. There are two suggested ways for this contrast to happen: One is the simultaneous contrast in which the changes occur when you look at the target object and the size of the visual angles subtended by extents that appear close to the target object; another is the successive contrast in which the changes occur when you first intently stare at the extents of nearby objects and then view the target object. Another popular explanation for the Ebbinghaus illusion is that the illusion is caused by linear perspective, that is, the larger surrounding circles look closer than the smaller surrounding ones; therefore, the central circle with the farther looking background is interpreted as bigger because a far object has to be bigger in actual size for it to have the same retinal image size as a near object. This phenomenon is accounted for by the "size constancy theory" or "taking into account hypothesis", that is, our brain takes the distance into account when interpreting the retinal image information; thus, a longer distance will make the perceived size of an equal retinal image larger.
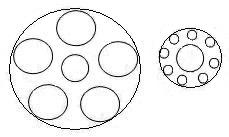
        However, I believe that the Ebbinghaus illusion is simply a variant of the Delboeuf illusion, and I have adequate evidence to prove my belief. What we see in the standard Ebbinghaus illusion are two identical middle circles enclosed by the outline of the surrounding circles, as shown in the figure on the left below. If we ignore the surrounding circles in the figure on the left below and concentrate only on the middle circles and their outlines, we will see a familiar figure, the Delboeuf illusion figure. I believe that the relative size of the surrounding objects plays a minimum or nonexistent role in the illusion. The Ebbinghaus illusion, like the Delboeuf and Ponzo illusions, is mainly caused by the visual field volume and the principle: The smaller portion of the visual field an object occupies, the smaller the object appears to be, and vice versa. To test this belief, all we need to do is to remove all the larger surrounding circles and replace them with small circles on their outline, and see what happens. As shown in the figure on the right below, the left middle circle still appears to be smaller than the right middle circle even though it is now surrounded by the circles the same size as the surrounding circles around the right middle circle. If the visual angle contrast works for the illusion, it still has to work; but not anymore. If the smaller objects in the surroundings remind you of a farther away distance, then these small surrounding circles still have to do so; but they do not. The sole factor contributing to the illusion in this figure is the sub-visual field volume as predicted by the principle gained from the analysis of the Delboeuf illusion.

                   

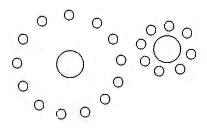
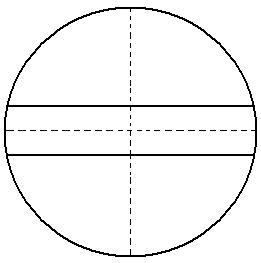
        Try this experiment yourself: look at a long straight wall. The wall seems to have straight and parallel lines when our line of sight is perpendicular to the wall, as shown in the figure below, where the parallel lines represent the top side and bottom side of the wall and the circle represents the conical visual field. If the apparent size of objects is caused by perspective, the appearance of the wall would be different. The wall would appear like a rugby football, that is, the middle is wider and both ends are narrower since the middle section is closer to our eyes and the walls on both sides are farther away from us as they extend further. The lines of the wall should converge on both ends when they are extending further away from our eyes as predicted by perspective and exampled by converging road or railway tracks extending to the horizon. The reason why the wall seems to have parallel lines when our line of sight is perpendicular to it is that the whole visible wall is inside the same conical visual field. As such, any part of the wall occupies the same portion of the visual field; therefore, the whole visible wall appears to have the same width from one end to the other. On the other hand, the same lines of the wall appear to be straight lines converging to a vanishing point on the horizon when our line of sight is parallel to the wall. The reason is that the conical visual field is not the same volume anymore. As we look further away, the visual field volume is expanding with increasing distance. As a result, the section of the wall at distance occupies a smaller portion of the visual field; and the lines appear to be smaller and closer to each other, or converging in relation to the larger visual field volume.  

       

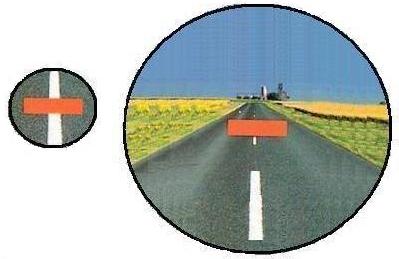
What I did was that I cut out the upper red bar with its surroundings intact. So the perceived distance of the upper bar is unchanged; it is still surrounded by the same-sized middle lines and side borderlines, and the objects on the horizon still look the same distance away. What has changed is the size of its background. Inspired by the principle: The smaller portion of the visual field an object occupies, the smaller the object appears to be, and vice versa, I have increased the visual field volume and as a result the proportion of the upper bar in the visual field has decreased. Accordingly, the size of the upper bar appears to be smaller than that before the manipulation of the picture. I did the opposite to the lower bar. Its visual field volume has been reduced and as a consequence its proportion has grown in the visual field, and it seems bigger than before. In the picture on the right above, the lower bar still looks close and the upper bar still looks distant; and the middle dividing white line under the lower bar still looks as big as before and the dividing line under the upper bar still looks as small as before. The perspective has not changed; the distance has not changed; and the surrounding objects' size has not changed. The only alteration I have made is the visual field volume and the proportions of the two bars in the visual field. At this point, someone might ask that in the original picture (on the left above) the frame size is the same for both bars, thus they should have the same visual field volume. How come the bars of the same size appear to be different in size with the same visual field volume? My answer is that the picture frame cannot represent the visual fields for these two bars. It is impossible for me to know the exact representation of the visual fields in our visual cortex, but I can postulate the possible visual field volumes for the bars with reasonable accuracy. The visual field for the upper bar is probably the horizon on the top, the road somewhere between the two bars at the bottom, and the crop fields somewhere close to the road on the sides. I think that this supposed visual field for the upper bar is reasonable. First of all, we seldom look beyond the horizon at the upper level of our vision. Secondly, if the visual field is close to the lower bar, it will interfere with the perception of the lower bar so that their visual fields have to be separated somewhere in the middle. Finally, when we stare at a road, we rarely notice the objects far off the road. As far as the visual field for the lower bar is concerned, it involves a little bit of imagination on the part of our brain. The upper level of the visual field is the horizon. The lower level of the field could be the bottom edge of the computer screen (or the bottom edge of the page if you view the picture in a book) since we can easily imagine that the road extends all the way to the bottom of the screen, or at least very close to the bottom of the screen. The sides of the field might be the borderlines of the road which extend well beyond the picture frame. As such, the visual field volume for the lower bar is much bigger than that of the upper bar. Accordingly, the perceived size of the lower bar in the picture has been reversed and appears larger than the upper bar which looks bigger in the original picture. If you are still not convinced, I am going to alter two more pictures to illustrate my point.
        Before I move on to tackle next two pictures, I would like to spend some time to elaborate on the imaginative power of our brain to extend the road beyond the picture, which is mentioned above. Look at the picture below. What you see initially are numerous disorganized black and white blobs. But, after you pay close attention to the picture for awhile, a picture of a Dalmatian dog sniffing under a stand of trees will emerge. This is an illustration of the concept of totality, which has been studied and advocated by the Gestalt psychologists. As we know, Gestalt is a German word that means, roughly, "whole configuration," or form. The Gestalt psychologists pointed out that whole patterns have emergent properties that are not shared by any of the component pieces. Even though we still do not know how exactly our brain achieve this feat, we do know that it can do it, as illustrated by the picture below. Simply put, our brain has the ability to connect the missing links to form a whole picture in our brain when the whole pattern is not present in the picture. Now some people might accept that our brain, similarly, has the ability to extend the road beyond the picture to obtain the whole pattern.

       

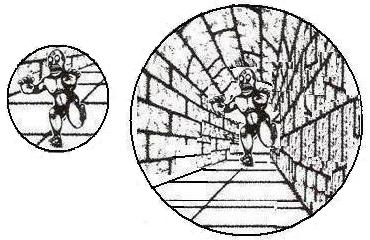
The picture on the left below is not only famous due to its inclusion in the textbooks, but also very impressive for the viewers since the chasing monster at the back looks a lot larger than the chased monster in the front and in addition the smaller chased monster looks scared as well. This picture is a demonstration of our brain's interpretative power. We can interpret a distant object of the same retinal size as bigger and also the facial emotion of a chased subject as terrified. As shown in the picture on the right below, I did exactly the same things to this picture as I did to the converging road picture above. I have altered the visual field volumes for the two monsters and left everything else intact; the visual field is enlarged for the chasing monster at the back and the visual field is shrunk for the chased monster in the front. Now the perceived sizes of these monsters are reversed.

The picture below has become famous also because it was used in Murray et al.'s study. The researchers in that study famously announced that two objects that project the same visual angle on the retina can appear to occupy very different proportions of the visual field if they are perceived to be at different distances; and a distant object that appears to occupy a larger portion of the visual field activates a larger area in V1 (the primary visual cortex) than an object of equal angular size that is perceived to be closer and smaller.Their behavioral measurements showed that subjects perceived the angular size (diameter) of the back sphere to be at least 17% larger than that of a front sphere of identical angular size, with the back sphere activating an area in V1 about 17% larger than the front sphere as well, a finding consistent with other studies showing that for a given angular size, distant objects appear to occupy more of the visual field than closer objects. They claim that they have demonstrated a relationship between the spatial extent of activation in human primary visual cortex and an object's perceived angular size, that estimating an object's behaviorally relevant size requires that its retinal projection be scaled by its distance from the observer or from other objects in the environment, and that extracting depth information from the texture and perspective cues in our stimuli requires that the information be integrated over a large area and probably necessitates the large receptive fields found in higher-order visual areas. It is thought that this depth information, once extracted, could then be used to rescale retinotopic representations in other visual areas. 

The importance of this study, in my opinion, lies in the fact that the illusory size changes are not just the subjective entities or mental constructions stemming from our interpretation or unconscious inference of the situation and environmental factors which do not exist in reality, and these illusory effects are also shown to exist in physical forms. For the first time in human history, it is proven that the so-called visual illusions are not psychological illusions once thought anymore; they have neurological and material bases now. It is interesting to note that their conclusion that an object that appears to occupy a larger portion of the visual field activates a larger area in V1 than an object of equal size is almost identical to the principle: The smaller portion of the visual field an object (of the same size) occupies, the smaller the object appears to be, and vice versa, which I have gained from analyzing the Delboeuf illusion. However, there is a key difference between their understanding of the visual field and mine, that is, the Murray et al. think that a distant object appears to occupy a larger portion of the visual field, meaning that the visual field gets smaller with distance rather than larger as illustrated earlier in the Delboeuf illusion section. To look at the visual field this way is understandable because it is consistent with the conventional wisdom. Let me quote a statement from a Psychology Wiki article: "As objects become more distant, they begin to appear smaller. This phenomenon is caused by perspective." So the perspective is considered to be the cause of our size perception. It is responsible for the converging road extending to the horizon, objects getting smaller at distance, and large appearance of a distant object of the same retinal image. If perspective can cause the roads, tunnels, and hallways to narrow down with distance (as shown in the three pictures above) and objects to shrink in appearance, it must be able to cause the visual field within which all these objects, roads etc. reside to contract as well. Looking at the picture above, we can see clearly the hallway is narrower when it is farther away. If we equate the width of the hallway with the visual field, it is not hard to imagine that the visual field is narrowing with distance. The back sphere looks a little bigger than the front sphere even though they have the same retinal size because the back sphere is located between a much narrower hallway so that it appears to occupy a larger portion of the visual field. Since the visual field is inversely proportional to distance, it is therefore more convenient to use distance, instead of the visual field, to scale the retinal image.
        The problem with our conventional wisdom lies in the fact that we have taken perspective and small appearing objects at distance for granted. Nobody has seriously questioned the cause of perspective itself because perspective is regarded as the cause of our size perception. However, linear perspective does not happen in nature; objects do not shrink when they are farther away from us. Perspective only happens in our eyes and consequently in our visual cortex. No perspective without a sentient being. Our visual field has a fixed angle. As such, when we look further away, this vision cone spreads out to cover a wider area of view. But this area still has to be focused onto the same-size retina, so obviously the image of a given object will take up proportionally less of our retina if it is 100 meters away than if it is 1 meter away. On the other hand, the opposite would happen if the visual field gets smaller with distance; the image of a given object will take up proportionally more of our retina when it is farther away. Instead of becoming smaller, objects would begin to appear larger when further away. This consequence is of course unacceptable and impossible. The effective way to resolve this paradox is to treat perspective as the effect rather than the cause of the visual field, that is, objects become smaller as they occupy a smaller portion of the widening visual field when further away. Since perspective is the effect of the visual field volume, distance becomes irrelevant to the size perception due to the close relationship between perspective and distance. In the picture below, the same-sized sphere at the back of the hallway appears smaller rather than larger than the front sphere. The far end of the hallway still looks as narrow as before and the back sphere still looks as faraway as before. What has caused the back sphere looking smaller is not the perspective, i.e., the distant looking hallway and smaller objects around it, but the expanded visual field in comparison to the shrunk visual field of the front sphere. In the picture below it is obvious that our brain has failed to scale the retinal size of the back sphere to make it look bigger based on the distance information. Thus, it can be concluded that the distance information is irrelevant for the size perception.

       

        As demonstrated earlier in the research done by Rock and Ebenholtz (1959), the observers perceive the central lines as equal in length no matter whether they are closer or faraway, as long as their proportion of the visual field is kept the same. Then how do we know which rectangle is closer to us since they both look the same size due to the same proportion of the visual field? Now we are facing a so-called depth ambiguity problem, which is often discussed in the textbooks. 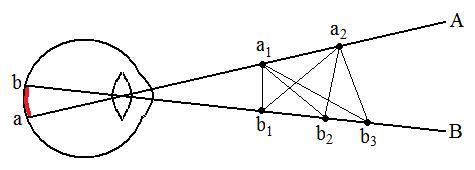The problem is that our depth perception has to be done using retinal images that have only two spatial dimensions -- vertical and horizontal. There is no third dimension for depth. To illustrate the problem of having a 2-D retina doing a 3-D job, consider the situation shown in the figure below. When a spot of light stimulates the retina at the point labeled a, how do you know whether it came from position a₁ or a₂ in the environment? In fact, it could have come from anywhere along the line labeled A, because light from any point on that line projects onto the same retinal cell. Similarly, all points on line B project onto the single retinal point labeled b. To make matters worse, a straight line connecting any point on line A to any point on line B (a₁ - b₂ or a₂ - b₁, for example) would produce the same image on the retina. The net result of all these possibilities is that the image on your retina is ambiguous in depth: the same retinal image could have been produced by objects at many distances from you. For this reason, the same retinal image can be given many different perceptual interpretations.

 

As a matter of fact, the depth ambiguity problem does not exist at all. It has been refuted already by a study conducted by Broerse et al. in 1992. They found that when observers projected afterimages of circular patterns onto a surface slanting away from them, the image were reported as being oval in shape. This finding shows that the images of a₁ - b₁ and a₁ - b₂ in the figure above are perceived as different in our cortex. If the image of a₁ - b₁ is a circle, the image of a₁ - b₂ is perceived as an oval shape instead of a circle as believed by those who are concerned about the depth ambiguity problem. Likewise, if the image of a₁ - b₁ is a square, the image of a₁ - b₂ will be perceived as a rectangle. Hence, our brain knows that a₁ and b₂ are at different distances from our eye. The reason why our brain can differentiate a₁ from b₂ is that a₁ and b₂ correspond to different visual field volumes. But, how exactly does our brain achieve this feat of differentiating a₁ from b₂?

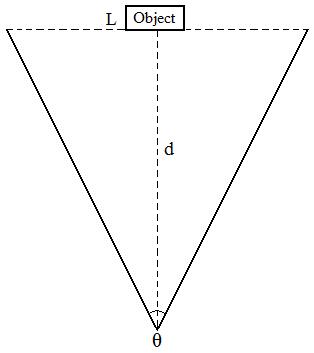
Let's look at the figure above. This triangular figure represents the top view of the conical visual field, within which L is the base of the conical field, representing visual field volume in one dimension (the diameter of the cone); d is the distance from the observer to the base of the visual field (also from the observer to the object); θ is the visual angle of a fixed value. In its simplest approximation, we can write these equations to illustrate the relationships between these factors:   θ = L / d   or   d = L / θ.  Since θ is a constant, we can simply do away with θ in the equation and obtain a simpler equation:  d = L.  Since L is fully represented on the retina and of course in the visual cortex, we have full information about L, or the visual field volume in one dimension in our brain. As such, we have full knowledge of d indirectly based on the information of L. So we just know that a₁ is closer than b₂ without relying on the distance cues or inference etc. (This issue will be dealt with in more details in the next article.)
        There is another approach which uses the binocular disparity to figure out the distance to an object. It is to use two images of the same scene obtained from slightly different angles by two eyes and then to triangulate the distance to an object. The triangulation is the process of determining the distance to a point by measuring two fixed angles, α and β as shown in the figure below; then we can use the following equations to calculate the distance to an object:

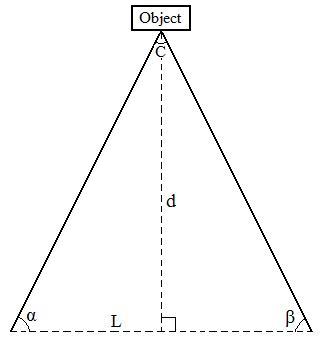
As you can see, my solution to determining the distance to objects (which I hope is the process actually used by our brain) is much simpler and therefore more parsimonious than the triangulation solution. No complicated calculation is necessary for my approach. The distance information is obtained simply from the visual field volume data which are available on the retina and in our visual cortex. Furthermore, as an object is farther away, the disparity of that image falling on both retinas will become smaller; thus it would be harder to utilize the disparity information to calculate the distance for a faraway object. On the other hand, my approach does not have this difficulty at a certain range (not beyond the solar system for instance).
        Don McCready states in his website that the magnitude of the visual angle illusion for the two equal targets on the page depends upon how big the difference would be between the perceived distance of the illusory 'objects' which the flat targets might portray in a pictorial depth (3-D) illusion that pictorial distance cues (mostly linear perspective) could generate for the given observer. That is, the size of the visual illusion for a particular 2-D flat pattern depends upon the observer's "ability" to convert some of the monocular distance cues into a pictorial (3-D) illusion that can provide different perceived distances for the illusory 'objects' the flat targets may be the 'images' of. As illustrated by the above three reversed pictures we do not possess the "ability" to convert distance cues into an illusion. We have the full knowledge of the pictorial distance cues in those 3-D pictures; but the so-called 3-D pictorial illusion is reversed from larger appearance to smaller appearance. In fact, these supposed 3-D pictures are still representing a 2-D flat pattern which is far from the real 3-D scene in the natural world. The pictorial pictures by the examples of the three pictures above are merely a weak imitation of the real 3-D world. For example, Murray et al.'s study reveals that the back sphere looks about 17% larger than the front sphere. However, according to McCready the back sphere is 5 times farther away from the viewer than the front sphere. If this is the case in the real world, the back sphere should look 5 times as big as the front sphere in diameter and 25 times as big as the front sphere in size (see Appendix A for details), which are 500% and 2500% larger than the front sphere. This is a very impressive difference. What has happened in those pictures is that the supposed depth cues and perspective are basically negligible and the artificially created sub-visual fields determine the perceived sizes of those objects, i.e., the far bar vs. the near bar, the chasing monster vs. the chased monster, and the back sphere vs. the front sphere.
        In the natural world we only have one general visual field, where everything is sized according to its place and portion in the visual field. The visual field volume is determined by the base of the vision cone, and the vertex is at the head between two eyes. However, for man-made artificial flat pattern illusions such as the Delboeuf illusion the solid black circles are located in the similarly sized comparable sub-visual fields. They are similarly structured and sized because the left and right black circles can be switched and still generate the same illusion. Thus, no matter where the solid circles happen to be projected in the brain, the result is the same. The brain cells can be seen as forming a map of the visual field (or retinotopic map), which we can treat as the general map of the general visual field. In many locations within the brain, adjacent neurons have receptive fields that include slightly different but overlapping portions of the visual field, which we can call the sub-visual fields in the sub-structures of the brain. These sub-structures that are responsive to various visual inputs are also organized into sub-visual field maps. Since there is limited space in each sub-visual field, which is like the film format, the perceived size of an object is determined by its portion in the sub-visual field. For example, the three photo pictures below were taken by a camera with 35mm film format. The top photo was taken by the camera with a focal length of 18mm, which is called the ultra wide angle lens that can cover more than 100° angle of view. The middle photo was taken with a focal length of 34mm, called the wide-angle lens covering about 60° angle of view. And the bottom photo was taken with a focal length of 55mm, which is the normal or standard lens, covering about 40° angle of view. The distance between the back blue bottle and the film (which can be treated as the equivalent of the retina) is the same for all three photos. The only difference between them is the angle of view, with a wider angle covering a larger sub-visual field. The blue bottle in the top photo looks smallest because it occupies the smallest portion of the sub-visual field among the three photos which have to fit in the same-sized film. Similarly, the three pictures above show that the objects within smaller sub-visual field such as the upper bar, the chasing monster and the back sphere appear larger; and those inside larger sub-visual field such as the lower bar, the chased monster and the front sphere appear smaller.

References

Related Information on the Web: