The Delboeuf, Ponzo and More Illusions

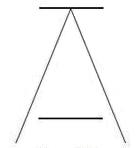
The Ponzo illusion is an important perceptual phenomenon for many illusion researchers because it is used to explain many other illusions such as the vertical-horizontal illusion, the Müller-Lyer illusion and the Moon illusion. It was first demonstrated by the Italian psychologist Mario Ponzo in 1913. He suggested that the human mind judges an object's size based on its background. He showed this by drawing two identical lines across a pair of converging lines shown in the 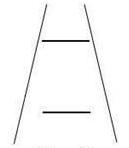figure on the left, which are similar to railway tracks or a straight road extending to horizon. 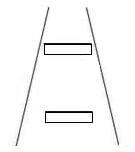The upper line looks longer because we are supposed to interpret the converging sides according to linear perspective as parallel lines receding into the distance. In this context, we interpret the upper line as though it were farther away, so we see it as longer; a farther object would have to be longer than a nearer one for both to produce retinal images of the same size. By the way, the standard Ponzo illusion figure on the left has two horizontal lines within the converging vertical lines; thus, the illusory effect is only one dimensional. If we change the horizontal lines into two identical rectangles as shown in the figure on the right, the illusory effect is now two dimensional. The upper rectangle looks not only longer but also wider; hence the upper rectangle appears to be bigger in two dimensions. The attribution of the Ponzo illusion to linear perspective is known as the perspective hypothesis. I am going to refute this hypothesis and linear perspective as a contributing factor as well.
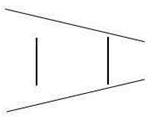
       First of all, let's make some changes to the standard Ponzo illusion figure to see whether the illusory effect will stay the same after we diminish or alter linear perspective. As shown in the figure on the left below, the standard Ponzo figure has been turned upside down; and as shown in the figure in the middle below the standard figure has been turned sideways (90^°). However, the same illusory effect still persists. This means that the illusion has very little to do with linear perspective because the illusory effect is still the same even though linear perspective cues have been diminished or eliminated. 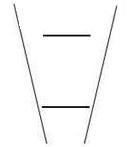In addition, if the Ponzo illusion corresponds to the real-life visual perception, the object at the end of the railway tracks where the parallel lines of the tracks join together would appear much larger than the closer object of the same retinal size. The figure on the right below shows us that this is not the case. The upper line at the converged end of the parallel lines does not induce the expected perceptual illusion at all, and it appears to be the same as the lower line in length. The reason for the disappearance of the illusory effect is because the upper line is no longer in the context of the converging lines; as a result, it has a totally different surrounding context or visual field volume.

        The figures above demonstrate to us that we should doubt the contribution of linear perspective in the Ponzo illusion. Now it is the time to look at linear perspective itself. Linear perspective is defined by this statement: As objects become more distant they appear smaller because their visual angle decreases. The visual angle of an object is the angle subtended at the eye by a triangle with the object at its base. The greater the distance of the object from the eye, the greater is the height of this triangle, and the less the visual angle. According to this definition linear perspective depends on the changing visual angles with distances. However, in reality we cannot perceive this visual angle at all. We can only perceive the light rays that have reached our retina and the extents of objects formed by those light rays. This visual angle cannot materialize on our retina by any stretch of imagination. Besides, this single visual angle can merely exist between our two eyes since it is claimed that we have the binocular disparity, meaning each eye has slightly different angle from the other. Therefore, the visual angle exists only as an approximation of a trigonometric function described by the light ray model which is an abstract mathematical idea and simply may not exist in the real world. It is a mental construction adopted for describing the size perception, not for explaining it.
        More importantly, the distance which has been conventionally considered a key factor in linear perspective is actually irrelevant. To prove the point, hold a picture or photo and focus on it, ignoring its surroundings. Now move the picture or photo close to you or farther away from you. Do you perceive the objects or specifically a human figure in the picture or photo as increasing in size when drawing your eyes closer to it or as decreasing in size when pulling your eyes away from the picture or photo? Also watch TV in total darkness. Now walk toward the screen and then walk backwards. Do you perceive a human figure on the screen as increasing in size when walking closer to it or as decreasing in size when walking away from the screen? The answer is that the human figure or objects in the picture or on the TV screen do not change in size when the distance between the viewed objects and your eyes have changed. But, if you now pay attention to the picture or TV screen and at the same time to its surrounding context or the visual field volume, you will notice the size of the picture or screen increases and decreases in relation to its surroundings. This simple experiment proves that our size perception has little or nothing to do with distance but the visual field volume. What has happened is that the frame of the picture or the TV screen acts as the boundary of the local visual field (which will be discussed in more details later); when the relationship between the objects and their immediate surroundings stays the same, in other words, when the proportion of the objects in the frame (or the visual field) is kept the same, distance has no effect on their perceived size whatsoever.
        In case that you are still not impressed by the simple experiments above, I am going to cite a well-publicized research done by Rock and Ebenholtz in 1959 to further prove the point. What they did was to ask observers to judge the lengths of the central lines in the two rectangles as shown in the figure on the left. As we can see, the central vertical lines are clearly different in length. However, when the observers 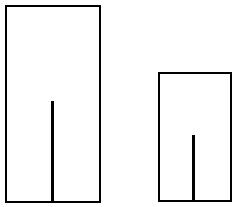viewed them separately in darkness, they tended to judge the two central lines as equal in length. This is because these central lines fill equal proportions of their frames. This experiment was designed to demonstrate that observers cannot judge the size of an object when there are no direct cues to depth in the visual scene. If they are correct and the direct cues to distance are available, the observers should be able to perceive the difference between the two central lines. When the larger rectangle is moved physically closer to our eyes, we should perceive the central line as growing longer because accommodation of our eyes provides direct cues to distance. But this is not the case. We do not perceive the central line as growing longer than the one in the smaller rectangle since the proportions have not changed. On the other hand, if we keep the central lines unchanged and expand the frames, the central lines would appear to shrink in size because they have decreased in proportion to the frames; and vice versa. Thus, we can change the perceived size of an object not by changing its distance, but by changing its visual field volume.
        Another contributing factor, in addition to linear perspective, is the so-called framing effect, in which objects that appear to fill an enclosing border appear larger than the same object surrounded by a larger frame, as shown in the figure on the left. The difference in the separation or gap of the horizontal bars from the framing converging lines helps to create the sense that the left bar, which is closer to the bordering lines, is larger than the right one. This effect of the Ponzo illusion can be seen clearly in 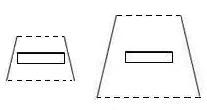the picture on the right which is popular due to its inclusion in many psychological textbooks. The upper red bar is closer to the road sides than the lower bar whose bordering lines are not even visible. This understanding of the framing effect, on the surface, seems close to my account of the visual field volume for the Ponzo and other related size illusions. However, the framing converging lines are not enough to explain the illusion; as a matter of fact, they can be misleading. As will be demonstrated later, the converging lines in the picture plays a minimum and perhaps even no role in the illusion. Consequently, there is a fundamental difference between the framing effect of those converging lines and the visual field volume that I believe plays a key role in the Ponzo and other related illusions.

References

Related Information on the Web: