Appendix A
The Perceived Size and Its Mathematical Equations
By Grant Ocean
Introduction1
Day and night our body and mind receive stimuli from the
outside world constantly. Our sensory systems by and large are doing a fine job
of obtaining the needed information from what is “out there” in order to take
necessary actions in response to the changing features in the physical
environment, which is vital for our very survival and existence. However, our
brain which is responsible for getting and perceiving the external stimuli
exists in a silent inner world surrounded by total darkness. This raises a
perplexing and enduring question, wondered by human beings for thousands of
years: How does the world out there get in? Or how do we acquire our
representations of the external world? So far the answer to this question is
far from adequate and satisfactory.
However, if the outside world projects a
picture-like or video-like two dimensional image on our retina, which is called
the proximal stimulus and is often quite different from the distal stimulus
that is the “real” physical object in the environment, as believed by many
psychologists and philosophers specialised in perception, how could preys and predators alike perceive distance which
demands a three dimensional perception? To address the question, the depth cues
such as retinal disparity, convergence, relative motion parallax, interposition
or occlusion, relative size, linear perspective, texture gradients, relative
clarity, relative height, light and shadow are proposed for the distance or
depth perception. And a perceptual process called “unconscious inference” is
suggested for the distance perception and perceptual constancy (including size,
shape, color, speed constancy etc.). It is a process of “inference” because the
visual system must figure out (or “infer”) the size of an object “out there”
and its distance by combining many depth cues and prior knowledge. It is
“unconscious” because the observer is not aware of knowing the size/distance
relation and other depth cues or of using them to perceive objective size and
distance, and to construct a three-dimensional image in the brain. But it is
not clear at all who or what is doing the inference. How could individual
cortical cells act like a conscious brain to use the depth cues identified by
numerous talented psychologists and artists over generations to figure out
perceptual constancy and distance? It is almost necessary to revive the concept
of homunculus (a tiny person) to achieve these tasks, including gazing at the
picture image or watching the video on the retina and then in the brain behind
the cortex, inferring object size, shape, speed, and distance, and constructing
and perceiving the 3-D image.
So far we have no clue as to the final stage of visual
processing. But we are willing to give too much credit and mysterious power to
our unconscious mind. It takes our conscious mind hours, even days, to finish a
thousand piece puzzle. How could it be possible for our unconscious mind to
reassemble a million piece puzzle instantaneously? In
my opinion, what we cannot achieve consciously is also difficult for our
unconscious mind. So how do our brains reconstruct the final images of the
outside world? Currently, there are many fundamental questions remaining to be
answered in the visual research. This paper is an attempt to address these
questions from the perspective of the natural laws governing our visual
perception.
Perceived
Object Size and Distance
In nature there is a basic physical law which is called the inverse-square law. Many other laws such as the Coulomb's law and Newton's Gravitational Law obey this basic law. In physics, an inverse-square law is any physical law stating that some physical quantity or strength is inversely proportional to the square of the distance from the source of that physical quantity.
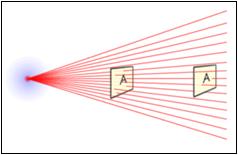
The diagram above shows how the inverse-square law works. The
lines represent the flux emanating from the source. The total number of flux
lines depends on the strength of the source and is constant with increasing
distance. For example, the stronger the light, the more flux lines or photons
it emanates. A greater density of flux lines or intensity, i.e., lines per unit
area, means a stronger field. The density of flux lines or intensity is
inversely proportional to the square of the distance from the source because
the surface area of a sphere increases with the square of the radius, expressed
by P = 4πr²I (P = total power; I = intensity, the power per
unit area). Thus, the strength of the field is inversely proportional to the
square of the distance from the source. Besides gravitation and electrostatics,
the intensity (or luminance or irradiance) of light or other linear waves,
e.g., electromagnetic and acoustic radiation, radiating from a point source
(energy per unit of area perpendicular to the source) is inversely proportional
to the square of the distance from the source; so an object of the same size
twice as far away receives only 1/4 the energy in
the same time period. In other words, the energy or intensity of light or other
linear waves follows the inverse-square behavior in the ideal three dimensional
context (vertical + horizontal + depth or distance
dimensions): It decreases by a factor of 1/4
as the distance r is doubled. On the other hand, the propagation of the
linear waves in two dimensions would follow an inverse-proportional behavior,
meaning that a physical quantity will decrease by a factor of 1/2
as the distance r is doubled.
The background assumption for my approach
is that our mind is a material entity so that it follows physical laws. So our
visual perception should follow the inverse-square law because our vision is
caused by the light rays, which are the material entity. To test the
assumption, I placed a measuring tape in metric system along the edge of a flat
tabletop longer than one meter. One end of the tape was placed at the edge of
one end of the table, and the value was set at zero. I attached a transparent
ruler to a stand so that it could stand up in a right angle to the tabletop and
also I could see through the ruler when measuring an object.
The first object I used for measurement
was an empty juice box that I had just finished drinking.2 The box was
10.7cm in height. First, I put the box at a distance of 50cm and the ruler at a
distance of 25cm. Then I placed one of my eyes at the zero point of the
measuring tape, with another eye closed. So my eye is the perceiving point; the
ruler is the measuring point; and the object (the juice box in this case) is at
a distance between the source and the perceiving point. After measuring the
height of the juice box at 50cm through the ruler at 25cm measuring point by my
eye at the perceiving point, the perceived height of the juice box was found to
be 5.35cm. Then I turned the juice box on its side so that its width became
10.7cm and placed it at 50cm. I also turned the ruler on its side at 25cm
measuring point. Looking at the juice box through the ruler and measuring its
width, I found the perceived width of the juice box to be 5.35cm as well,
consistent with the symmetrical principle. In summary, the original size of the
object is 10.7cm both in height and in width; both the perceived height and
width are 5.35cm at a distance of 50cm and at a measuring point of 25cm.
Next I placed the juice box at 100cm and
kept the ruler at the same 25cm measuring point. By doing exactly the same as
before, both of the perceived height and width were found to be 2.675cm. To
compare, we divide the perceived height and width at 50cm distance by the
perceived height and width at 100cm distance:
5.35cm ÷ 2.675cm = 2
The result shows an inverse-proportional distance behavior
because the object’s height or width is propagated in two dimensions (vertical
or horizontal + depth). The intensity (the perceived height or width of the
object) has decreased by a factor of ½ as the distance from the object is doubled from 50cm to
100cm. And to compare the perceived sizes of the object (size = height ×
width) at both 50cm and 100cm distances, we divide the perceived size of
the object at 50cm by the perceived size at 100cm:
(5.35cm × 5.35cm) ÷ (2.675cm × 2.675cm) = 4
The result demonstrates an inverse-square behavior. The
perceived size or intensity of the object has decreased by a factor of 1/4 as the distance from the
object is doubled from 50cm to 100cm because the object’s size is propagated in
three dimensions (vertical + horizontal + depth). Thus far the
background assumption has been confirmed to be accurate in predicting the
visual perception, specifically the relationship between perceived object size
and distance. As a result, suffice it to say that our visual perception indeed
follows the inverse-square law as far as this case is concerned.
Now I need to explain why I chose a
measuring point at 25cm instead of putting the ruler at 1cm from the perceiving
eye. The reason is that it is easier to measure the object at a closer distance
from the object and a farther distance from the perceiving eye; the perceived
height or width would be too tiny to be accurately measured if the ruler were
placed too close to the eye. As a matter of fact, the measuring points do not
affect the relationship between perceived object size and distance. To avoid
the longer numbers after the decimal point, I replaced the juice box with a
square shaped object measured 10cm on each side. When the object was placed at
50cm and 100cm respectively and perceived at 20cm measuring point, the
perceived height or width was 4cm at 50cm distance and 2cm at 100cm distance
respectively. To calculate the difference between the perceived heights or
widths at these two distances and the difference between the perceived sizes at
these two distances, we get:
4cm ÷ 2cm = 2
(4cm × 4cm) ÷ (2cm × 2cm) = 4
As you can see, the results we get at 20cm measuring point
are exactly the same as those obtained at 25cm measuring point. No matter how I
changed the distances of the object and the measuring points, the results were
always the same as long as one distance was twice the other distance. I made
many more measurements using objects of different sizes at different measuring
points and distances. And I also asked others to make the measurements. The
results were quite consistent.
Based on the measurements, I can
demonstrate the inverse-proportional distance behavior of perceiving object’s
height or width. When we place a 10cm high object at 50cm distance and perceive
it at 50cm measuring point, the perceived height is still 10cm, 100% of the
original height. If we perceive the object at 45cm measuring point which is a
10% increase in distance from the source, the perceived height is now 9cm which
has decreased by 10%. Likewise, at 40cm measuring point, a 20% increase in
distance, the perceived height is 8cm, a 20% decrease; at 35cm, a 30% increase
in distance, the perceived height is 7cm, a 30% decrease; at 30cm, a 40% increase
in distance, the perceived height is 6cm, a 40% decrease; at 25cm, a 50%
increase in distance, the perceived height is 5cm, a 50% decrease, and so on.3 Due to the fact
that the perceived height or width of an object is always counterbalanced by
distance, we have come up with the equation for the perception of object’s
height or width:
H = Ph ·
d or
W = Pw · d
(1)
where H is the actual
height of an object; Ph is the perceived height of the
object; and d is the distance from the object. Similarly, W is
the actual width of an object; Pw is the perceived width of
the object; and d is the distance from the object. When H = 10cm,
Ph = 0.2cm, and d = 50cm,
10cm = 0.2cm × 50cm = 10cm
So
the equation works. If we change the equation to
Ph = H / d
and replace H with 10cm
and d with 50cm, we get:
Ph = H / d = 10cm
/ 50cm = 0.2cm
Thus the perceived height is the measurement you would get
when perceiving the object at 1cm measuring point. Therefore, we can conclude
that the perceived height or width is obtained by setting the measuring point
at one unit of the measuring instrument such as one meter, one centimeter, or
one millimeter. We can also change the equation to
d = H / Ph
d = H / Ph = 10cm
/ 0.2cm = 50cm
Hence we can find out any variable in the equation if we know the values of other two variables. Also because of this inverse-proportional distance behavior, we can get
H = Ph1 · d1 =
Ph2 · d2 or
W = Pw1 · d1 = Pw2
· d2
(2)
where Ph1 is the first perceived height; d1 is the first distance; Ph2 is the second perceived height; d2 is the second distance; Pw1 is the first perceived width and Pw2 is the second perceived width. For example,when the perceived height is 0.2cm at 50cm distance and 0.1cm at 100cm, we get
10cm = 0.2cm × 50cm = 0.1cm ×
100cm =10cm
Taking the measuring point into
consideration, we can change the above equations to the following forms:
![]() or
or
![]() (3)
(3)
![]()
![]()
The equations that we have discussed thus far are applicable
to the same object or objects with the same height and width. However, for the
objects with different heights and widths, the proportion equation below should
be used:
![]() (4)
(4)
where
H1 is the actual height of the first object; H2
is the actual height of the second object; Ph1 is the
perceived height of the first object; d1 is the distance from
the first object; Ph2 is the perceived height of the second
object; d2 is the distance from the second object. In the
proportion equation, if H1 = 10cm and H2 =
30cm, so the ratio between H1 and H2 is 1
to 3. The ratio between Ph1 · d1 and Ph2
· d2 is always 1 to 3 correspondingly, no matter
where the two objects are. For example,
![]() (a)
(a)
![]() (b)
(b)
In the example
(a) the distance is 50cm from the first object and 100cm from the second
object; and in the example (b) the distance is 80cm from the first object and
40cm from the second object. As you can see, the results are always the same
regardless of the distance differences of the two objects.
If we divide H1/H2
on both sides of the equation, we get:
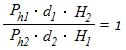 or
or ![]()
We can verify the equation by putting values from the
example (a) in it and get:
0.2cm × 50cm × 30cm = 0.3cm ×
100cm × 10cm
300 = 300
With the equation (5), we can find out the value of one
variable if we know the values of all the other variables. Take the example (a)
for instance:
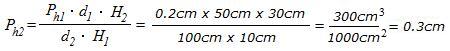
Since the size of an object is calculated by its height times its width, we have the following equations for the object size:
S = (Ph · d) (Pw
· d) or
S = Ph · Pw · d2
(6)
where S is the actual size
of an object; Ph is the perceived height of the object; Pw
is the perceived width of the object; and d is the distance from the
object (throughout this paper d always stands for the distance; so I am
going to omit defining it from now on). If we have an object with 10cm in
height and 10cm in width, at a distance of 50cm, we have
100cm2 = 0.2cm ×
0.2cm × (50cm)2 = 100cm2
We can simplify the above equation to
S = Ps ·
d²
(7)
where Ps is the
perceived size of the object and is the product of perceived height times
perceived width.
Similar to height or width of an object,
the size of an object equals the perceived size of the object times the
distance squared no matter where the object is, thus
![]() (8)
(8)
where Ps1 is the
perceived size of the object at d1; Ps2 is
the perceived size of the object at d2.
For example, when the perceived height is
0.2cm at 50cm distance and is 0.1cm at 100cm, we get
100cm2 = 0.2cm ×
0.2cm × (50cm)2 = 0.1cm × 0.1cm × (100cm)2 = 100cm2
For the objects that have different sizes, we have to use
the proportion equation as below:
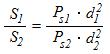 (9)
(9)
where S1 is the
actual size of the first object; S2 is the actual size of the
second object. The equation tells us that the ratio of the actual sizes of two
objects remains the same no matter how different their distances are. The
variation of the equation can be written as:
![]() (10)
(10)
If we measure the perceived size of an object at a measuring
point more than one unit, we use the following equations:
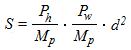 (11)
(11)
or
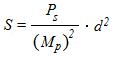 (12)
(12)
Speed,
Distance and Length
The relationship between perceived speed and distance is
similar to that between perceived width or height and distance. The reason for
the similarity is that the movement from point A to point B can be seen as a
certain length (either width or height) per unit of time. The speed is defined
as the distance traveled in a specific time interval; so it can also be looked
at as the width or height traveled in a unit of time. In our everyday lives
most moving objects are traveling horizontally with the exception of rocket
launching which travels vertically. A moving object, for instance, can be
measured at point A as zero meter, and then measured
again at point B, 10 meters away from point A, after one second has passed.
Thus, the speed of the object is 10m/sec. We can also say that the width of the
movement is 10 meters long measured in the time interval of a second.
As a result, we are able to derive the
inverse-proportional distance equations for speed based on the equation (1) for
the object’s width:
Sp = Ps
· d
(13)
Sp = Ps1 · d1 = Ps2 · d2
(14)
where Sp is the actual speed of a
moving object; Ps is the perceived speed of the moving
object; and Ps1 is the perceived speed at the first distance d1;
Ps2 is the perceived speed at the second distance d2.
Accordingly, the perceived speed of a moving object appears to be slower when
the distance is farther away. For example, if the actual speed of a moving
object is 10m/sec and it is measured at 5m distance, based on the equation (13)
we get:
![]()
As a
result, the perceived speed of a 10 meter per second moving object at a
distance of 5 meters is 2 meters per second. This result is same as that of an
object with 10 meters in width being measured at a distance of 5 meters with
the measuring point set at one measuring unit, that is, the perceived width is
2 meters. The perceived speed of the same moving object would be merely
0.1m/sec if it is perceived at a distance of 100 meters away. What our eyes are
actually perceiving should be much smaller (or slower) if the objects are measured
at a closer measuring point. Therefore, to emulate the actual perception by our
eyes in order to understand motion perception we need to measure the movement
as close to our eyes as possible. If we used millimeter instead of meter as the
measuring unit, the perceived speed of the 10m/sec moving object at 5 meters
and 100 meters would be just 2mm/sec and 0.1mm/sec in our eyes respectively.
The equation (14) tells us that the
actual speed remains the same no matter how different the perceived speeds are
as long as they are counterbalanced by the distances.
The equation (13) can help explain the
phenomenon of motion perception, such as the motion gradients. As you look at
right angles to the direction of motion, like looking out the side window in a
moving car, the objects close to you seem to move backwards faster than those
farther away from you. And beyond a certain point, the objects seem to move
along with you instead of moving backwards. The farther away an object, the
faster it appears to move with your car. The equation tells us that all the
fixed objects on the ground are moving backwards relative to the direction of
your moving car. But the perceived speed of the objects at a long distance is
so minuscule that we do not perceive their backward movement and that we
perceive them as moving along with the car. The smaller magnitude the perceived
speed of an object due to the greater distance, the swifter it seems to move
along. Because all the fixed objects are moving backwards relative to your
motion no matter how slowly they appear to move at a great distance away from
you, sooner or later they will move out of your sight after you drive for
awhile, with the farthest object disappearing last.
Besides the distance, the perceived speed
is also influenced by the object’s size, especially the length of an object
because the movement of an object is usually in one direction. The length of an
object is its width when it is moving horizontally, and is its height when
moving vertically. If an object has 20 meters in width and moves horizontally
at a speed of 10m/sec, it would take two seconds for the object to move out of
its original spot. On the other hand, at the same speed it would take one
second for a 10 meters long object to move out of its original spot, and half a
second for a 5 meters long object to do so. Imagine that you stare at a point
and an object is moving across that point. The object has uniform color so that
no reference frame can be used on the object. When the head of the object
crosses the point, you would not be able to detect movement before the tail of
the object passes the point. Thus, a shorter object will take less time to pass
the point and hence be perceived as moving faster in comparison to a longer
object if the two objects move at the same speed. When the length of the
objects is used as unit for measuring movement in a time interval instead of
regular measurements such as kilometer, meter, and centimeter in metric system,
we get:
![]() (15)
(15)
where Ps is the
perceived speed of a moving object; Sp is the actual speed of
the object; l is the length of the object. For an object of 20m long and
moving at 10m/sec, by using the equation (15), we get:
Ps = Sp
/ l = 10m/s ÷ 20ml = 0.5 lengths/sec
For a 10m long object and a 5m long object at the same
actual speed, we get respectively:
Ps = Sp
/ l = 10m/s ÷ 10ml = 1 length/sec
Ps = Sp / l = 10m/s ÷ 5ml = 2 lengths/sec
Thus, in 10 seconds the 20m long object will cover a space
of 5 lengths (10 sec × 0.5 lengths/sec = 5 lengths); the 10m object will
cover 10 lengths; and the 5m object will cover 20 lengths respectively. On the
basis of these calculations, it is obvious that the perceived speed is
inversely proportional to the length of the objects. This finding is consistent
with the observation that the longer objects such as a train seem to move at a
slower pace even though their actual speed is same as other shorter objects. To
combine the two equations (13) (15), we have:
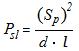 (16)
(16)
where Psl
is the perceived speed of the length; Sp is the actual speed
of the moving object; and l is the length of the object. This equation shows
that the perceived speed of the length of an object is inversely proportional
to both its distance and length. For example, when Sp =
10m/s, d = 50m, l = 5ml,
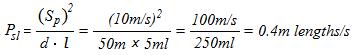
And when Sp = 10m/s, d = 50m, l = 10ml,
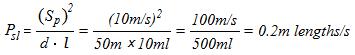
Accordingly, doubling the length of the object will reduce
the perceived speed of the length by half when everything else is the same; or
likewise, doubling the distance from the object will reduce the perceived speed
of the length by half while everything else being equal. This equation can help
explain why faraway large object such as the moon seems to move very slowly. No
matter how fast you are driving the car at night, the movement of the moon is
barely noticeable when you look at it through the side window. You would detect
the position changes of the moon relative to the side window frame only after
you have driven for awhile. Let’s put in exact values in the equation (16) to
illustrate the perceived speed of the length of the moon. The average distance
of the moon from the Earth is 384,400km and the Moon’s diameter is 3,476km. If
you drive your car at a speed of 108km per hour or 30m per second, the
perceived speed of the length per second is 6.72 × 10-13m lengths,
which would be too infinitesimal to be detected. After you have driven for 10
minutes, the perceived speed of the length is 2.42 × 10-7m lengths;
for an hour, 0.00087m lengths, if we assume that the reference frame or
measuring point which is the side window in this case is set at one meter and
the moon and earth are not moving themselves.
Another phenomenon that can be explained
by the equation (16) is that large objects tend to appear stationary and
smaller objects seem to be moving. When we watch a spot within a frame, we tend
to perceive the spot as moving against the background regardless of which is
moving, the spot or the frame. Similarly, the moon appears to be stationary in
a clear sky. When framed by a moving cloud, the moon will appear to race across
the sky while the cloud appears stationary. The perceived length of the spot or
the moon is much smaller in comparison to the frame or the cloud; let’s assume
it is a hundred times smaller. According to the equation (16), the spot or the
moon would seem to move 100 times faster than its background; in contrast, the
movement of the frame or the cloud (moving at a pace 100 times slower in
comparison) would be too diminutive to be noticed.
Furthermore, the equation (16) can help
explain the autokinetic effect, in which a single
spot of light will appear to move about, sometimes oscillating back and forth,
sometimes swooping off in one direction or another, if you stare for a few
seconds at it in a completely dark room (no frame of reference can be used to
determine that the light spot is stationary). As we know, our eyes do not stay
fixed in one position and they move about due to the physiological nystagmus. If the actual speed of a person’s eye movement
is characteristic and stable, then the perceived speed of a single spot under
the circumstance of no reference frame depends on the distance from the spot to
the observer and the length (or diameter) of the spot. Accordingly, the smaller
the spot of light and the closer it is to the observer, the faster the
perceived speed; on the other hand, the moon or a single star in a dark empty
sky does not appear moving at all because they are very big and far away.
Therefore, the autokinetic effect can be calculated
and predicted by the equation (16).
Perceptual
Constancy
The goal of
perception is to obtain information about the world around us, not about images
on our sensory organs. Specifically, the goal of visual perception is to
acquire information about the visible world, not about images on our retinas.
Since the distal stimulus and the proximal stimulus are considered quite
different according to the traditional viewpoint, the concept of perceptual
constancy has been introduced to refer to the ability of our visual system to
perceive an unchanging world despite the constant changes that occur in the pattern
of stimulation on the retina as the result of different viewing conditions in
addition to the idea of depth cues. The perceptual constancy includes size and
shape constancy, brightness and color constancy, speed constancy and so forth.
I agree that the perceptual constancy is important because it enables us to
identify things regardless of the angle, distance, speed, and illumination by
which we view them. However, the traditional view is that the perceptual
constancy is achieved by obtaining additional information from the outside
world such as distance cues for size and shape constancy and context cues for
brightness and color constancy, whereas I think that
the proximal stimulus has already contained almost all the information needed
for the perceptual constancy. The proximal stimulus is the replica of the
distal stimulus but on a smaller scale.
Size constancy refers to the ability of
our visual system to perceive the true size of an object despite size
variations of its retinal image. For example, you hold one of your hands close
to your eyes and another hand at an arm’s length; you perceive them as being
the same size although one hand is actually smaller than the other by many
times. When I went to an electronics store and stood by a TV set, I could tell
which ones in the background (over 5 meters away) are approximately the same
size as the set in front of me among many sets of different sizes. This amazing
feat is vital for our survival and that of other animals. Otherwise, we might
mistakenly attack a large animal which appeared small at a distance. In fact,
the equation (8) contains all the information for size constancy. This equation
tells us that the results will always be the same as the actual size of the
object no matter what distance it is at. Although I doubt that our brain has
the ability to do the multiplication and square calculations, I believe that it
can achieve the feat of size constancy by using and combining these ratio
formulas: Ph1 : Ph2 =
d2 : d1 and Pw1 : Pw2
= d2 : d1, derived from the equation
(2), which show that the ratio of the perceived heights or widths is equal to
the inverse ratio of the distances from the object. All our brain needs to do
with these formulas is to obtain the ratio of Ph1 to Ph2
or Pw1 to Pw2 and then reverse the
ratio for the distances. Or it can use Ph1 :
d2 = Ph2 : d1 and Pw1
: d2 = Pw2 : d1, also
derived from the equation (2), to infer size constancy.4 With these formulas
all our brain needs to know is that Ph1 (or Pw1)
is inversely related to d1 and directly related to d2
and Ph2 (or Pw2) is inversely related to d2
and directly related to d1. Finding relationships and
associations and doing comparisons should be the strength of our brain even
though it may not be able to do mathematics like a computer.
We perceive an object’s actual shape
correctly even when it is slanted away from us, making the shape of the retinal
image (or pattern of photons) substantially different from that of the object
itself. For example, a circle tipped away from us projects an elliptical image
onto our retina; a rectangle tipped away projects a trapezoidal image. However,
we usually perceive them accurately as a circle and a rectangle slanted away in
space. As a matter of fact, shape constancy is closely related to size
constancy. Therefore, the equations used for size constancy also contain all
the information for shape constancy. For instance, when we look at a framed
rectangle shaped picture on the wall from an angle, the edge toward us appears
longer than the edge on the other side because the other edge is farther away
from us. The reason why we perceive this picture as a rectangle rather than a
trapezoid can be explained by the equation (2) or the ratio equation derived
from it: Ph1 : Ph2 = d2
: d1. These formulas tell us that the perceived
heights (Ph1, Ph2, . . .) of the object are
always the same as the actual height of the object (H) as long as they
are counterbalanced by distances, i.e., the first perceived height (Ph1 ) is balanced by the second distance (d2)
and the second perceived height (Ph2) is balanced by the
first distance (d1), and so forth. As a result, the various
perceived heights of the object are always the same in spite of the distance
differences.
Speed constancy is our ability to perceive the true speed of
a moving object despite variations in the perceived speeds. It is very
important for us to function safely in the environment, especially in the age
of automobiles. When you are driving a vehicle, you need to know the actual
speed of other vehicles in order to make a safe move such as turning into a
main street, changing lanes, crossing a road or railway tracks. Since the
perceived speed is closely related to the perceived height or width, speed
constancy is also related to size constancy. Similarly, the equations (13) and
(14) contain all the information for the speed constancy, meaning that the
perceived speeds (Ps1, Ps2,
. . .) are always the same as the actual speed of the object as long as
they are counterbalanced by distances. Therefore, we are able to ascertain the
true speed of a moving object on the basis of its perceived speeds if we can
figure out its distance from us.
Discussion
One possible practical application for
the equation (1) or equations (3) (4) is to find the actual height of an
object.5 Using
these equations to measure the height of a distant object is
simple because all you need is a measuring tape that will be used to measure
the distance and the perceived height as well in case you do not have a ruler.
(Of course, a ruler with smaller units would produce more accurate
measurements.) The measurement of height by this method is more accurate than
all the other methods except for the trigonometric method, i.e., Height =
distance × tan (angle). But, in comparison, the trigonometric method is
more complicated and needs a calculator and protractor in addition to a
measuring tape to complete the measurements and computation. Moreover, apart
from simplicity, another advantage of using the equation (1) over the
trigonometric method is that we can use the width version W = Pw
· d to find out the actual width of the object in addition to its actual
height. Therefore, we can employ the equation (7) to discover the actual size
of any object, which the trigonometric method is incapable of doing.
The formulas d = W / Pw and
d = W · Mp / Pw based on the equations (1) (3) can
be used to measure the distance given that the actual height of an object is
known. Take estimating the height of a cliff as an example. The traditional
method is to throw a rock over the cliff and time its fall, and to use the
equation d = ½gt2 to calculate the distance
traveled by the rock, which is equal to the height of the cliff. First of all,
this equation is more complicated to calculate, and you need a stopwatch and
have to remember the value of g (9.8m/s/s) in order to do the math.
Secondly, each person has different reaction times to stop the watch, and you
need to know how to deduct the traveling time of the sound; hence, the
estimated height of the cliff is not very accurate. On the other hand, by using
the equations above, all you need is a ruler. Find a tree branch or similar
object and measure its length (w); then throw it over the cliff and
measure its perceived length (Pw). Dividing the branch’s
length by its perceived length you will get the distance from the top of the cliff
to the ground or the height of the cliff. This method is simpler and more
accurate.
The human and animal brains are thought
to be able to conduct quite complicated calculations like a computer. For
instance, consider what happens when a bird of prey has a small mammal on the
ground within its sights. It is thought that success of capture depends on not
only that the hunter knows where its target is, but also that it can estimate
where the target will be if it is moving. So the accuracy of the calculations
has to be sufficient for the tracks of the hunter and its prey to coincide.
However, to make the capture a success, the brains do not need to operate like
a computer; all the hunters need are the equations (13) (14) and to know that
the perceived speed of the prey is inversely related to the distance. By using
the equation, the hunters should be able to adjust their actions when they are
approaching the target. The perceived speed of the prey is increasing while
they are getting closer to the target. Also, they need the equation (1) to
obtain an accurate estimate of the actual size of the mammals on the ground. It
is quite dangerous to attack a mammal that is much larger than themselves by mistake.
There was a challenging question asked by
the supporters of the geocentric theory: How come we could not detect the
position changes of the stars if the Earth were orbiting around the Sun? The
equation (16) can provide a more precise answer than that of the parallax
method. The stars are light years away from the Earth, ranging from 4.3 to a
couple of hundreds of light years, as far as the naked eyes can see. Let’s take
the brightest star in the night sky “Sirius” as an example, which is 8.6 light
years away (1 light year = 9.46 × 1012km) and is 2.363 × 106km
in diameter. The Earth’s orbital speed around the Sun is about 30km per second
or 2,568,000km per day. By putting these values in the equation (16) and
calculating, the perceived speed of the length is 4.68 × 10-18m
lengths per sec; 3.52 × 10-8m lengths per day; and 0.00000352m
lengths in 10 days, if we assume that the Earth is traveling in a direction
perpendicular to the star and the measuring point is set at one meter.
Therefore, we cannot detect any position changes of the stars by our naked eyes
even though the Earth is traveling at a fast speed by our earthly standard.
The ability for human beings and animals
to estimate the distance, and the actual size and speed of an object at
different distances should be innate, as indicated by the equations which are
probably built in the brain system in one form or another; otherwise, it is
hard to imagine how they are going to survive in the environment. For example,
Gibson and Walk (1960) tested the response of infants (6-14months olds) to a
visual cliff. When the mother called to the child from the cliff side and from
the shallow side successively, almost all the infants crawled off onto the
shallow side but refused to crawl onto the deep side. Furthermore, chickens
tested when less than 24 hours old never made a mistake by stepping off onto
the deep side; and goats and lambs always choose the shallow side as soon as
they could stand. It seems that the brain has the innate ability to infer the
distance, the actual size, and speed, as discussed earlier in the paper.
However, the accuracy of these estimations can be improved through experience.
Zeigler and Leibowitz (1957) conducted an experiment
comparing the performance of eight-year-olds and adults in judging the size of
objects at different distances. At a distance of 10 feet, both children and
adults show close to perfect agreement between their judgment of size and the
actual size of the object. But at greater distances, the children show
increasingly less accuracy while the adults’ judgments remain quite accurate.
Obviously, the more accurate judgments on the part of adults are due to more
experience they have had during their longer lifetime. This means that
someone’s ability to tell distance, the size and speed of a moving object can be
improved through intensive training. The implication is especially important
for athletes, pilots, or anyone who needs to know exactly where the targets
are, how far away they are, and how fast other players or objects are moving
about.
Our brain is thought to engage in
parallel processing, i.e., constructing our perceptions by integrating the work
of different visual teams, working in parallel, instead of step-by-step serial
processing as most computers do. The concept of parallel processing is suggested
by some cases of visual disabilities caused by brain damages. I am going to
discuss two such cases cited by Hoffman (1998).
Case one: Looking at an American flag,
Ms. W is able to see lines and stars. But “it’s like you have one part here and
one part there, and you put them together to see what they make.”
Case two: Ms. M, having suffered stroke
damage near the rear of both sides of her brain, can no longer perceive
movement. People moving about a room seem “suddenly here or there but I have
not seen them moving.”
For the proponents of the parallel
processing idea, the case one indicates that there is one team in the visual
cortex responsible for the perception of forms; and one team for the perception
of motion (case two). However, these peculiar cases can all be explained by
some of the equations in the paper.
The case one can be explained by the
equation (7). It becomes harder for us to ascertain an object’s form or pattern
when the perceived size of the object is getting smaller due to the increased
distance from the object. For example, when you look at the signs from a
distance, you can tell whether it is written in English or Chinese, or any
language you are familiar with, and you can see the lines, curves, even shapes;
but you cannot tell what words are on those signs. From far away you can see
the main features of a face such as the eyes, nose, mouth, and you can tell
whether a face is a female’s or a male’s, or a young person’s or an old
person’s; but you cannot recognize a familiar face. For the purpose of checking
the eye sight, the letter “E” and its rotations (up, down, left, and right) are
used for the examined to identify which side the concavity is on. When the
printing is smaller or when it is farther away, it is harder to recognize its
form or pattern, even though the lines are recognizable. These examples are
similar to Ms. W’s experience in which she could see lines and stars but could
not recognize what form or pattern these lines and stars make.
The case two can be explained by the
equation (13). You can hardly notice any movement of a distant object; but you
can tell that it has changed positions after a period of time. The best example
is the behavior of the moon when you are driving, as discussed earlier. You
cannot perceive any movement when you look at it. But you will notice the
position shifts of the moon after a dozen minutes of driving. This example is
almost identical to Ms. M’s experience.
It is not easy to convince a suspicious
mind that these equations can indeed explain what happened to the perceptions
of those in the two cases above, even though there is an obvious correspondence
between their experiences and the equations, because it appears that the
crucial factor in the equation, the distance, has seemingly nothing to do with
their conditions. However, under closer scrutiny we can find a common ground.
What the increased distance has done to the perceptions is to reduce the light
energy or photons that reach the retinas; as such, less signals or information
will be transferred to the visual cortex. Accordingly, we can speculate with a
great deal of certainty that what the damaged brain has done to the two
individuals in the above cases might be to prevent a portion of the signals
from registering at the visual cortex. Therefore, the common factor for both
the increased distance and the damaged brain is the reduction of information in
the visual cortex; somehow the results are the same although they are achieved
through totally different means. Nevertheless, the profound implication is that
the perceptions of form, motion, and depth may not require separate or parallel
processing, but can be handled by our brain all at once.
Finally, I feel necessary to point out
that the mathematical equations often have power beyond the wisdom of their
discoverers. I have only discussed the possible applications and implications
of these equations as far as my knowledge and imaginations can reach. And my
interpretations of these equations may not even be appropriate or correct.
Their potentials will not be fully realized until they are verified, accepted,
and further explored by the science community.
In conclusion, based on the facts
acquired from the experiments designed to test the background assumption, it
has been confirmed that the objects’ sizes perceived at different distances
follow the inverse-square law, and a series of mathematical equations are
formed in the process. These equations have demonstrated that they have the
explanatory and predictive power for a wide range of observations, including
almost all the main phenomena in the areas of sensation, perception, and
attention. They indicate that our perception is governed by the natural laws
more than subjectivity. They may also have a profound impact on our
understanding of behavior and mental processes, and the brain and mind.
Endnotes
1. This appendix is a paper that I wrote many years
ago before I put my mind to the visual illusions. The background assumption and
some of the mathematical equations in this paper have influenced my approach
and thinking regarding the size illusions and many other issues. As a matter of
fact, I told myself to use this background assumption to solve the puzzles of
visual illusions to see if it works. Thus, the perceptual illusions are the
testing ground for my insights gained in this paper. Therefore, it is
imperative to read this paper in addition to your readings of the size illusion
articles. I have changed my mind with regards to some of the ideas in this
paper; but I still include these out-of-date ideas here. I want the readers to
witness the development of my ideas over the years.
2. Yes, the juice box is an odd object for
experiment. I mentioned the juice box in the paper to record and remind me of
my "Eureka moment". I had been thinking about the background
assumption, i.e., our minds should work as the other natural objects and follow
the natural laws, for many days, but did not find a way to prove it. When I saw
the empty juice box on the coffee table in the early morning, all of a sudden I
got the idea to measure the juice box to see if the perceived size of it
follows the inverse-square law. I put the juice box in the middle of the coffee
table and measured it with my pinching thumb and index finger, and then put it
at the end of the coffee table and measured it the same way. I found out that
the perceived height of the juice box in the middle of the coffee table is
twice its height at the end of the table. At this very moment, I realized that
the perceived size of objects follows the inverse-square law even before I
measured the perceived width of the juice box, because I knew nature obeys the
symmetrical principle. I think that my ecstasy at that moment is comparable to
that of Archimedes when he leapt out of his bathtub and ran through the streets
of Syracuse naked, believing that he had just found the principle of buoyancy.
Some people might dismiss this experiment as unnecessary because it is a fact
in the perception field that the retinal size of an object reduces twice as
much when its distance doubles, many people could easily predict the results of
this experiment. It is most likely that many people had observed this
phenomenon before me. I simply observed what everybody else observes. However,
I thought what everybody else had not thought of about this phenomenon. I linked
this observation to the inverse-square law, as a result linking our mind to
nature.
3. These measurements may seem simple and
unnecessary; many people in the perception field could probably predict the
results. However, these innocent measurements become the basis on which I might
have solved, in my opinion, some tough size illusions such as the Moon
illusion, the Ames Room illusion, and Emmert's law.
The measuring point here becomes the converging point in the later-on model to
explain the size illusions. At the time I had no idea that I could use these
measurements for something more important. All I intended to do was to prove
the relationship between the perception and the inverse-square law.
4. Interestingly, I find that Professor McCready
has done similar things, i.e., ratio computing, to figure out linear size
constancy. When I wrote my paper, I was unaware of his work. So we had similar
ideas independently. But I have already changed my mind about this idea and
believe that our brain can achieve size constancy without computing or ratio
balancing. I have kept this "out-of-date" idea to show that my
current ideas have developed based on prior less mature ideas. Einstein once
said something like this: any idiot can make things more difficult, complicated
and violent, and it takes a genius to make things easier and simpler. I am not
an idiot and definitely not a genius; but I am ready to admit my mistakes and
learning from my mistakes. When I find a way to make things simpler, I am
willing to abandon my previous ideas no matter how hard I worked on them and
how proud I was about those ideas.
5. I was concerned with practical application
at the time because I thought that it is a general consensus in the scientific
community that any theory or model should have some kind of practical usage.
Now I am simply pursuing a understanding for its own
sake, without any practical concerns.
References
Gibson, E. J., and Walk, R. D. (1960). The “visual cliff”. Scientific American, 202, 64-71.
Hoffman, D. D. (1998). Visual intelligence: How we create what we see. New York: Norton.
Hubel, D. H., & Wiesel, T. N. (1968). Receptive fields and functional architecture of monkey striate cortex. Journal of Physiology (London), 195, 215-243.
Ross, H. (1975, June 19). Mist, murk, and visual perception. New Scientist, 658-660.
Sperry, R. W. (1985). Changed concepts of brain and consciousness: Some value implications. Zygon, 20, 41-57.
Walker, R. D. (1968). Monocular compared to binocular depth perception in human infants. Science, 162, 473-75.
Zeigler, H. P., and Leibowitz, H. (1957). Apparent visual size as a function of distance for children and adults. American Journal of Psychology, 70, 106-09.
<<
Previous Home
Next >>