For a picture to simulate the real world,
it has to show a larger
visual field volume for the back sphere and a smaller one for the front
sphere, which is impossible for a static picture. In the real world, if
we focus on the front sphere or on any fixed point ahead of the front
sphere as the camera did,
the back sphere will appear to be the same
size in diameter as the front sphere, assuming that the back sphere is
five times bigger in diameter and five times farther away from the
viewer than the front sphere.
The
perceived sizes of the front and back spheres will not change as long
as the converging point is in front of the front sphere, which is the
case for the picture above.
This result is determined by the equation
Ps = S / d.
You can also confirm this outcome by focusing on your near hand and
then perceiving your far hand to check whether it changes size from
moment to moment.
But, according to
Murray et al.
the back sphere is perceived by observers to be 17% larger than the
front sphere on average. This is impossible in the real world. The
reason why the back sphere is perceived slightly larger is that the back
sphere happens to be located in a smaller sub-visual field in
the picture and our brain manages to extend the picture further to
generate a larger sub-visual field for the front sphere.
In reality, when we converge our eyes on the back sphere, it
will appear to be five times bigger in diameter than the front sphere
instead of a tiny 17%. This picture further proves that a 2-D picture
cannot accurately represent real 3-D world at all.
One of the distinguishing
features of Renaissance art was considered to be its development of
highly realistic linear perspective.
Giotto di Bondone (1267–1337) is credited
with first treating a painting as a window into space, which started the tradition of perspective drawing.
Looking at objects through a window has the converging point
fixed at the window; as a result, one cannot focus on any object beyond
the window. We are actually perceiving everything outside the window
with micropsia, that is,
all the objects appear smaller than their actual sizes and even
smaller when they are further away, which is the essence of linear
perspective. Hold up your right hand close to your right eye and look
through your pinched thumb and index finger with your left eye closed.
In so doing, everything seems to be smaller and you feel that
you can squeeze those objects with your fingers. Now view a house
across the street between your thumb and index finger.
The house is perceived as small as the space between your
pinched fingers. Then move your fingers aside and focus on the house
and the two pinched fingers with the same space between them.
All of a sudden, the house becomes thousands times bigger than
before. Similarly, if you can move the window through which you are
looking at a house across the street aside, the house will appear to be
much bigger than the window.
All in all, the artists before Renaissance were not totally
wrong when they painted the human figures the same size at different
distances because they had emphasized the aspect of size constancy.
The artists since Renaissance are not totally right when they
are painting the objects based on perspective because they put emphasis
merely on the aspect of micropsia. In the real 3-D world we have both
aspects for our size perception.
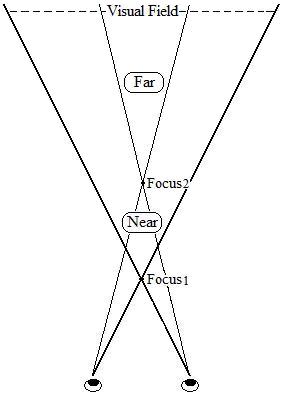
The picture on the right is an example given by
Don McCready to show the difference between the linear size and the angular size,
which we have already encountered in the second section of this article. In

this example, we are looking at a house across the street through a nearby window.
McCready claims that we experience both the linear size and the angular
size comparisons at the same time, along with the distance comparison. We can say that the house is bigger than the window,
referring to the linear sizes of them; and we can also say that
the house looks smaller and farther away than the window, referring to
their angular sizes.
However, this is a 2-D picture; thus there is no way that we
can tell the house is actually bigger than the window, except that we
can guess the actual size of the house based on our knowledge that a
regular house is usually much bigger than a regular window,
but this guessing is not based on our perception. This situation is similar to the Ames Room illusion.
Even though you know that the twins should have the same size,
you still perceive the far corner twin as being smaller in size. It is
because you look at the house and the twin through a fixed converging
point, i.e., the window and the viewing hole.
As I have stated earlier, if you move the window aside or poke your head outside the window,
the house will look a lot larger than the window because you
can converge your eyes on the house when the converging point is not
fixed on the window. This is a fundamental difference between the 2-D
picture and the real 3-D world.
Also McCready claims that in everyday conversations "looks larger"
often refers to an angular size comparison rather than a linear size
comparison.
In this picture and also in the real world we cannot compare
the sizes of the house and the window as long as we are at the viewing
position as shown in the picture.
We are focusing on the window, so the size of the window we
perceive is approximately its actual size, which is similar but not
equivalent to the linear size as discussed before.
On the other hand, we are perceiving the house through the
window, i.e., perceiving it by means of a fixed converging point at a
distance, which is similar but not equivalent to the angular size.
It is of course hard or even impossible to compare the actual
size of an object with the perceived size of another object at a
distance. If we move the window aside and focus on both the house and
the window,
then we can compare the actual size, or the perceived size at a
close distance, of both objects. And if we can focus on a fixed point,
such as a viewing hole or a camera,
which has equal distance to both the house and the window, then
we can compare the perceived size of both objects at an equal distance
from our focus. In comparison, it would be easier to compare the actual
sizes by focusing on both objects.
Finally, McCready claims that when we say one object "looks larger" than another,
we most
often are using the verb "looks" to describe not the perceived linear sizes, but
the perceived angular sizes for them. Actually, I think that when we say objects "look larger" or "look smaller",
we simply mean the way objects look from a fixed converging
point. For instance, when we say that the house across the street looks
small through the window, we mean the way the house looks as viewed
through the window;
when we say that one twin looks smaller than another twin in
the Ames Room, we mean the way they look through the viewing hole. And
when we say that everything looks small as viewed between our pinched
thumb and index finger,
we mean the way they look between our fingers. The window, the
viewing hole, and the space between thumb and index finger are all
fixed converging points.
Without the fixed converging point, we can just focus on
objects at a close range and determine approximately the actual sizes
of the objects. Of course, we cannot say that an object looks larger or
smaller when we have already found out that it actually is large or
small.
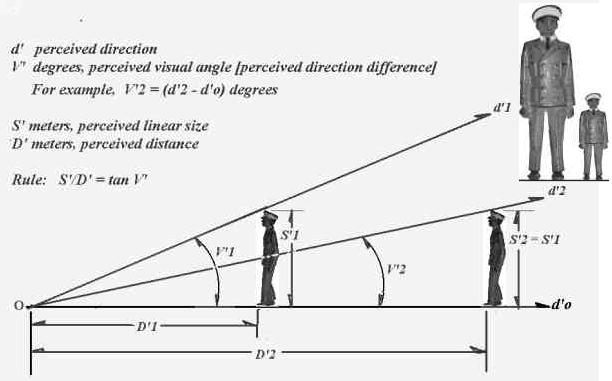
Don McCready and other perception researchers have proposed various ways to solve the problem posed by the Gregory's photo,
which is similar to the two men drawing at the top right corner of the diagram above.
They claim that the picture easily
leads to a percept of two men at the same perceived distance.
It is because our perceptual system performs a process known as
the equal distance scaling resulted from an "equidistance assumption"
or an "equidistance tendency".
And the perceived linear
height of the man on the left is twice that of the man on the
right because his perceived angular subtense is twice as large. To make the men's linear sizes look equal,
the S' values could be scaled equal by the (cognitive) familiar
size cue to linear size or identity constancy if the observer knows
their heights; and if the men are unfamiliar, that scaling could occur
due to an "equal linear size assumption".
In addition, many complex equations and computing processes
have been proposed to maintain the linear size constancy (for details,
see McCready's
web page). In comparison, my solution to the problem is much simpler and perhaps more effective.
The two men of the same height will look the way as shown at
the top right corner of the diagram above when the viewer focuses on
the near man or a converging point in front of the near man such as a
viewing hole or a camera lens.
But the two men will look the same height as soon as the viewer focuses on both of them.
By doing both, the viewer would know the fact that both men
have the same height and one man is twice as faraway as the other, as
discussed earlier. To repeat my solution to size constancy at the end
of this article is to reiterate that there are numerous efforts to
solve the problem,
but the simplest approach could be the appropriate one if you believe in parsimony.
In the
previous article we discussed the visual field volume and in this article I have introduced another important concept, the converging point.
Equipped with these two ideas, we can explain adequately a
well-known phenomenon called Emmert's law and can also solve the most
important size illusion of all and most complicated one, the Moon
illusion.




 this example, we are looking at a house across the street through a nearby window.
this example, we are looking at a house across the street through a nearby window.