Since afterimages do not change in size at the retina, what we see in the apparent changes of size noted by Emmert is conventionally regarded as a compensatory mechanism at work. It is compensating for what would normally be changes of size of the retinal image, but as the afterimage remains unchanging, size constancy gives illusory changes of size. The constancy scaling is believed to be set by several 'distance cues' such as convergence of the eyes, geometrical perspective, and the graded texture and falling of sharpness ('aerial perspective'), which are believed to be associated with increasing distance of a viewed object. Correspondingly, afterimages change their size with changes of convergence angles of the eyes, or with perspective. Any cue to distance can set the brain's perceptual compensatory size constancy scaling mechanism.
        Emmert's law can be expressed by the following equation:   Perceived size = Retinal image size × Perceived distance.
        Since we are already familiarized with McCready's work, which has been discussed in many occasions in the previous article, let's use his equation for Emmert's law: S' = D'·θ, where S' is the perceived linear size of an object; D' is the perceived distance of the afterimage's projection; and θ is the retinal size of an afterimage. In the equation, θ remains constant, and S' will change depending on D'. As such, the perceived size of an afterimage is proportional to its perceived distance. However, a simple proportional relationship is deemed by many researchers to be unlikely at very large distance. Therefore, the fact that Emmert's law holds over a huge range of distance, which is seemingly far beyond what size scaling can explain, leads to the conclusion that the law is still not fully understood.
        In the light of the monumental study of Murray et al., which found that the perceived size of an object has corresponding cortical activity in the primary visual cortex (V1), I have done a simple calculation. If we say that the perceived size of an afterimage is proportional to its perceived distance, then doubling the distance would more than double the perceived size. The reason is that the size used in the equation above is not the full size of an afterimage, but merely the diameter or height. Hence, the full size of an afterimage is proportional to the perceived distance squared. Let's say that an afterimage occupies one part out of a million in V1. If that afterimage is projected onto a surface at a distance of 1000 units, the perceived full size of the afterimage would use up the whole V1; and we could not perceive the projected afterimage anymore beyond 1000 units because the perceived size of the afterimage has already exceeded the capacity of V1. However, our experience and various experiments tell us that we still can perceive the afterimage at a distance far beyond 1000 units. Thus the equation and the linear relationship between the perceived size of an afterimage and the perceived distance are demonstrated to be incredible.
        The brain's perceptual compensatory size constancy scaling mechanism is supposed to operate like this: our brain 'projects' a retinal afterimage onto a surface on which the afterimage remains the same size. However, the perceived size of the afterimage on a distant surface would be perceived as smaller than before when it is reflected back onto the retina if the original afterimage on the retina is projected onto the distant surface unchanged. This is incoherent because an afterimage on the retina should not change size every time it is projected to a different distance. Hence our brain uses the perceived distance based on various cues to enlarge the perceived size of the afterimage to keep the retinal afterimage constant. If this explanation of Emmert's law is correct, then we should be able to measure the increased perceived size of an afterimage with increased distance, as shown in S' = D'·θ. To test this hypothesis, I set a ruler at a fixed distance from my right eye, and then measured the perceived size of the afterimage, obtained by staring at the black circle above for 20 or more seconds, at different distances. The outcome of measurements is that the perceived size of the afterimage is exactly the same at different distances. Therefore, the hypothesis is refuted and the equation and the conventional explanation of Emmert's law are further discredited.
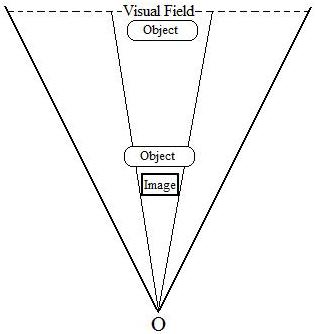
        I think that the afterimage on our retina is projected out just like the visual field as shown in the diagram below. I have envisioned the visual field spreading out like a flashlight before. The projected afterimage of the black circle above is literally like a flashlight when viewing it on a surface in a dark room. The projection of an afterimage can also be envisioned as a movie projector. In the diagram below the Image is the perceived afterimage. The thinner lines beside the Image are the edges of the projection. The size of the Image will not change no matter how far the projection lines are extended because it is measured at a fixed spot on the projection track. The fundamental distinction between my diagram below and the conventional understanding of Emmert's law is that the perceived size of an afterimage, I believe, is caused by actual physical change of the afterimage on a surface, not by the brain's processing system, the so-called compensatory size constancy scaling mechanism. As I said, if this mechanism or system exists, we should be able to measure the changes of the afterimage. Richard Gregory believes that there is a change in retinal stimulation for each wall or screen lying at a different distance, for their images will be different. But we cannot measure these image changes even if we set the measuring instrument very close to the eye which is supposed to be the measurement of the retinal size. Likewise, we might not find any cortical activation change in V1 either when the projection of an afterimage is viewed through a fixed converging point.
       

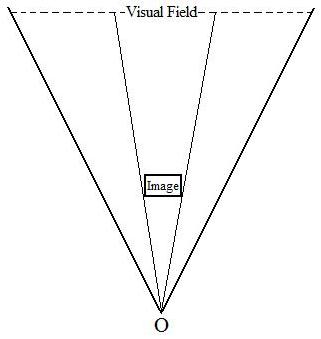
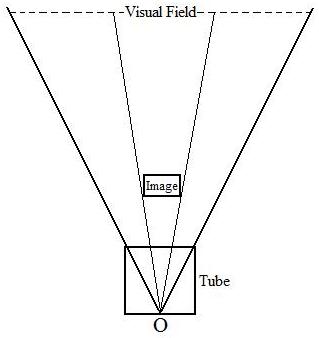
        To further prove my point, I observed the afterimages through a paper tube. The perceived size of an afterimage is always the same no matter where the afterimage is projected onto. This result can be depicted by the diagram below. While viewing through the tube, the converging point is fixed at the O position and the converging angle is fixed as well. As such the visual field volume is fixed at a certain distance.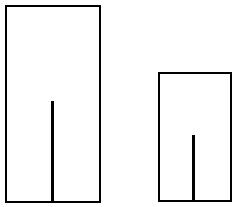 For an afterimage to appear the same size at various distances, it has to spread out in proportion to the visual field, as shown in the diagram below. In so doing, the projected afterimage at any distance viewed through the tube will have the same proportion in the conical visual field. Even though the absolute size of the afterimage changes with distance, it changes proportionally with the visual field. As a result, the portion of an afterimage remains the same within the visual field; and the perceived size of it will stay the same as well. This result has been confirmed by the study of Rock and Ebenholtz (1959), which I have mentioned many times in the previous articles. Observers in their study could not tell which central line was longer, as shown in the figure on the right, when they were shown the rectangles separately, because the central lines in both rectangles have the same proportion in the rectangles. I believe that this is the only way that an afterimage can remain the same size on the retina and in the cortex. Imagine that the visual field is expanding as usual with distance and the projected afterimage is the same at a longer distance. When the projection is reflected back on the retina, its retinal size will be smaller because it will occupy a smaller portion of the retina space, and the situation is the same in the cortex. I guess the basic rule is that the retinal size of an afterimage must stay the same by all means. The best and only way to do so is to spread out the same way as the visual field. Here the visual field is the determining factor which causes the projected afterimage to expand with distance, and at the same time to keep the afterimage staying the same on the retina.


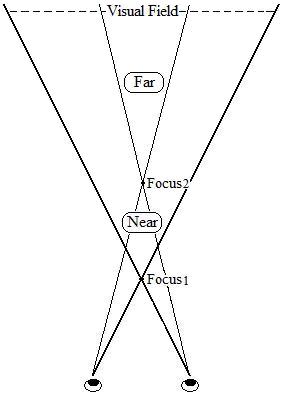
        Then, if the retinal size of an afterimage is the same when projected onto the surfaces of different distances and our brain does not compensate for the shrinking effect of the distance, why do we all perceive the afterimage as becoming larger when projected onto a more distant wall or screen? Well, here comes the second important concept, the converging point, which I have used to explain the Ames Room illusion. As shown in the diagram on the left below, if we move the Focus1 forwards and place our converging point at the Focus2, the sub-visual field will become much smaller for the far object which in turn will be perceived as larger since it now occupies a larger portion of the reduced visual field volume. When we view the afterimages which are projected onto the surfaces of different distances, we tend to focus on them. As a consequence, we always place the converging point close to the projected afterimages. The expanding afterimage with distance will be perceived as larger. The situation is similar to the picture on the right below. (Now you have to imagine the scene in the real 3-D world rather than the 2-D picture.) When viewed through a fixed converging point such as a camera aperture, the back and front spheres are perceived as the same size if the back sphere is five times bigger in diameter and five times further away. Likewise, the projections of an afterimage are perceived as the same size while viewed through a tube. Instead of two positions in the picture, the projected afterimages are perceived as the same in any position since they change in proportion to the visual field volume. When you look at the back sphere without the camera, it appears to be much bigger than the front sphere, which is similar to looking at the afterimages on the wall without the tube.

        Now I would like to discuss a study done by Broerse et al. (1992). In that study, when observers projected afterimages of circular patterns onto a surface slanting away from them, the images were reported as being oval in shape. But this did not occur when similar afterimages were projected onto the slanting rear wall of an Ames Room. Instead of appearing as ovals, the afterimages remained circular. They reasoned that it appears as though the actually-slanted rear wall of the room not only looks as if it were normal to the line of vision, but also that it functions as if it were in such an orientation as far as a projection surface for afterimage is concerned. However, my explanation is that the Ames Room is viewed through a viewing hole; as such the afterimage is perceived as the same at any distance as demonstrated by the experiment I have conducted with a paper tube. Hence the afterimages on the rear wall of the Ames Room remain circular because the slanted wall or different distances will not affect the perceived size of the afterimages. This result has nothing to do with perceiving the rear wall of the Ames Room as being cubic. On the other hand, when we can view the slanting surface without a viewing hole, we can focus on the surface and hence bring the converging point close to the surface. Thus, the end of the circle that is projected onto the further surface will appear bigger and wider than the other end that is projected onto the nearer surface.
        Based on our new understanding of the phenomenon, Emmert's law should be defined as the proportional increase of perceived size of an afterimage with increasing visual field volume.