The Converging Point and Camera
To understand why we have such an illusory perception of the figures, i.e., the woman on the right looks much shorter than the woman on the left, in the photo on the left below, we have to look at the diagram on the right below once again. We can regard the Focus1 as the aperture of a camera, which is similar to the viewing hole of the Ames Room and the opening of a tube. Once the converging point and converging angle are fixed, the visual field becomes wider for the farther objects; thus they will appear smaller. What has happened to the photo on the left below is that the camera "knows" (or simply follows the rules) that the woman on the right has a larger visual field volume around her and hence has to appear smaller on the film.
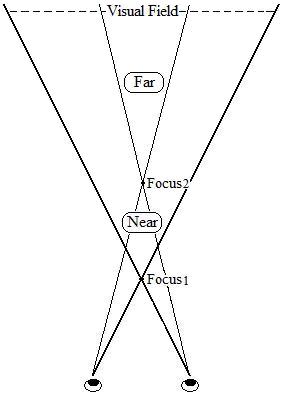
The camera
somehow "perceives" the full conical visual field which is like a
flashlight spreading out from the aperture of the camera,
as shown in
the diagram on the right above in which the visual field is diverging
from the Focus1.
On the other hand, the photo on the left above looks
like it being recorded by a tunnel vision, i.e., the visual field is
the same for near and far objects. For a tunnel vision objects would
appear the size as their actual size no matter where they are; thus
objects would not change size at all.
The film has a limited space
(35mm for standard format); therefore, it is impossible for a film to
record the full conical visual field as the camera "sees".
As we know,
to produce a scene somewhat close to what we actually see in the real
world the photographer has to connect many photos together side by
side. So a photo can merely record a small part of the visual field.
The camera does not record the sizes of objects on the film according to the
limited visual field allowed by the film; it does so based on the full
conical visual field it "sees" in the real world and the portions of
objects in the visual field.
What we see in a photo is not the true
relationship between objects and visual field volume; what we see
is the result of this relationship in the real world. The illusory effect in the photo
above is due to the fact that what have been recorded on the film does not reflect the real visual
field volumes associated with the figures and the photo is two dimensional.
It is the same with the photos of the Ames Room.
Someone might point out that it is ridiculous for a camera to "perceive" the visual field and make a decision before the images reach the film. One can use the old size equation θ = S / D to make the point, that is, for a certain size S, an object's size on our retina and also on the film (since the retina and film are always considered equivalent by perception researchers) is determined by the distance D. As such, the size of objects on the film is always smaller when they are farther away and always larger when they are closer to the camera. The film records this size variation obediently without exception. The size of objects on the film has nothing to do with the conical visual field volume outside the camera. Well, let's look at the pictures below which we have seen in the previous article. The top photo was taken by the camera with a focal length of 18mm, covering more than 100° angle of view. The middle photo was taken with a focal length of 34mm, covering about 60° angle of view. And the bottom photo was taken with a focal length of 55mm, covering about 40° angle of view. The distance between the back blue bottle and the film is the same for all three photos. However, the size of the back blue bottle is quite different on the film depending on the sub-visual field volume regulated by the angle of view of the camera. These pictures demonstrate that the objects' size can certainly alter on the film when distance between them is unchanged. This deals another blow to the old size equation θ = S / D. By the way, the front pink bottle in the photos does not change as much in size. We can consult the diagram above for the answer. When the converging angle changes, the portion of near objects in the visual field does not change as much as far objects' portion in the changing visual field.
Someone might point out that it is ridiculous for a camera to "perceive" the visual field and make a decision before the images reach the film. One can use the old size equation θ = S / D to make the point, that is, for a certain size S, an object's size on our retina and also on the film (since the retina and film are always considered equivalent by perception researchers) is determined by the distance D. As such, the size of objects on the film is always smaller when they are farther away and always larger when they are closer to the camera. The film records this size variation obediently without exception. The size of objects on the film has nothing to do with the conical visual field volume outside the camera. Well, let's look at the pictures below which we have seen in the previous article. The top photo was taken by the camera with a focal length of 18mm, covering more than 100° angle of view. The middle photo was taken with a focal length of 34mm, covering about 60° angle of view. And the bottom photo was taken with a focal length of 55mm, covering about 40° angle of view. The distance between the back blue bottle and the film is the same for all three photos. However, the size of the back blue bottle is quite different on the film depending on the sub-visual field volume regulated by the angle of view of the camera. These pictures demonstrate that the objects' size can certainly alter on the film when distance between them is unchanged. This deals another blow to the old size equation θ = S / D. By the way, the front pink bottle in the photos does not change as much in size. We can consult the diagram above for the answer. When the converging angle changes, the portion of near objects in the visual field does not change as much as far objects' portion in the changing visual field.

The four photos below were taken by a 35mm still camera at a constant distance from the objects. But the size and perceived distance are quite different on the film. These photos are further evidence that the visual field volume modified by the converging point and angle can alter the size of objects from the same observational position. The first photo from the left was taken with a 28mm lens, and the following photos were taken with progressively longer lenses and narrower view angles. The longer lens means that its aperture can be moved closer to the objects, which is equivalent to moving the converging point closer to the objects by our eyes. Coupled with the narrower angle of view, the sub-visual field volume has been progressively reduced in the photos from the first to the last; as a result, the objects appear to be the largest in the last photo. If we really think that cameras are similar to our eyes, they follow the rules just as our eyes do. Nonetheless, there is a difference between camera and our eyes, that is, cameras can have various angles of view at a fixed aperture position and our eyes have only one converging angle at one converging point.



