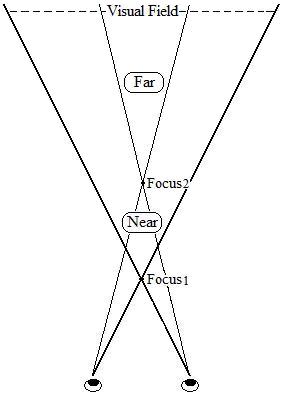
The diagram above also illustrates that if you only focus on the near object and do not switch your focus to the far object, the perceived size for the nearer and farther objects would be quite different. As you can see in the diagram, the visual field space represented by the thicker lines on the outside extended from the Focus1 is much wider for the far object. This is my explanation for micropsia, i.e., if you focus on a nearer object, the sub-visual field volume will be larger for the farther objects (as shown in the diagram above); therefore, the farther objects appear to be smaller, vice versa.
        The conventional understanding of micropsia cannot account for the Ames Room illusion in the photo below. According to the conventional understanding, if we converge our eyes on the near figure, which is the woman on the left in the photo, then the far figure, the man on the right, will look smaller. However, even if we focus on the man in the far corner only, the man appears just as small as before. As a matter of fact, no matter where you focus your eyes on in the Ames Room, the appearance of the two individuals is the same. As discussed earlier, the perceived size of the figures in the Ames Room is determined by the equation Ps = S / v. So the sub-visual field volume is the determining factor in the illusion. Besides the shape of the room, the Ames Room illusion is created by observing the objects or figures in the room through a viewing hole. This viewing hole acts as the converging point. It is impossible for us to extend this converging point beyond the viewing hole; otherwise, we would have to look through the solid wall to converge our eyes on objects beyond the viewing hole. Again, let's look at the diagram above. If we regard the viewing hole of the Ames Room as the Focus1, the objects farther away from this converging point have a wider visual field around them and hence occupy a smaller portion of the field; as a result, the smaller portion of the visual field an object occupies, the smaller the object appears to be. Therefore, the Ames Room illusion is not caused by the distorted shape of the room, but by the fixed converging point and a wider visual field for the far corner figure.

        Hold up one of your hand, with the back of the hand facing you. When you move this hand back and forth in front of your eyes, the hand does not seem to change size. This size constancy is maintained by keeping the converging point close to the hand at different distances, as discussed earlier. Now take a tube and put it around your eye, then view the same hand through the tube with another eye closed. (You can use the paper tube inside the toilet paper, or cup your hand by curling your fingers to make a hand tube.) This time you get a different result. The hand seems to shrink when it moves away from your eye no matter how hard you try to focus on it. The reason is that the converging point is fixed at the opening of the tube and cannot be extended beyond this point. The visual field, as a result, is expanding as the hand is moving farther away from the eye; again the smaller portion of the visual field an object occupies, the smaller the object appears to be. Even though you know clearly that your hand is moving away from your eye (since you are doing the moving yourself) and there is no distorted room to fool you about the depth, the full knowledge of increased distance in this case fails to compensate for the perceived size of your extended hand. The old equation of the size perception S = θ · D cannot explain this phenomenon, that is, both S and θ are decreasing while D is increasing. Furthermore, no existing theory can explain why the perceived size of the same moving hand changes when viewed through a tube, but does not change when viewed without the tube. As far as I know, the converging point and visual field volume I am proposing here are adequate to account for these phenomena. Again, it is not the cubic perspective that overrides your perception of size constancy; it is the fixed converging point by means of the viewing hole that overrides your perception of size constancy in the Ames Room.