Home


The Ames Room Illusion

By Grant Ocean

The Converging Point and Size Constancy

        To begin with, let's conduct the following exercise: (1) Hold your eye and a ruler one unit from the eye stationary, then measure the size of an object that is moving away from the ruler. (2) Hold your eye and a far object stationary and move the ruler back toward the eye from the object, then measure the size of the object. (1) and (2) are equivalent and the perceived size Ps is decreasing in both cases. Again, (1) hold your eye and a ruler one unit from the eye stationary, then measure the size of an object that is moving toward the ruler. (2) Hold your eye and a far object stationary and move the ruler forth toward the object, then measure the size of the object. (1) and (2) are equivalent and Ps is increasing in both cases.
        The above exercise seems to be simple and obvious; but it gives us a brand new understanding of the size perception (see Appendix A for details). Usually we only pay attention to the size variations when we approach or recede from objects; and we do not pay attention to the size changes induced by changes of an observational frame of reference (or measuring point) such as a ruler moving towards and backwards from objects. As a matter of fact, this phenomenon was discovered over a century ago and referred to as Hering's maneuver. That is, hold your thumb out at arm's length directly below some far object, e.g., a picture on the wall; and maintain fixation and focus on your thumbnail while moving your thumb closer to you. Notice how the far object appears to shrink in size so long as focus is maintained on the near thumbnail. However, this phenomenon has been misunderstood since Charles Wheatstone who lived in the same century as Hering. He reported that when the eyes are accommodated and converged for near vision, targets of some fixed angular size look smaller than they do when accommodation is relaxed and the optic axes are parallel, and that this perceptual effect is related to the operation of the eye's muscular mechanisms rather than to awareness of distance per se. Since then the phenomenon has often been called accommodation or convergence micropsia. But more often than not, the phenomenon is called oculomotor micropsia, which is defined by Don McCready based on his new perceived equation as following: While one is looking at an object that subtends a constant visual angle θ, if one then accommodates and converges one's eyes to a distance much closer than the object's distance, the object's perceived visual angle θ′ decreases. Here the phenomenon is attributed to the new concept θ′ caused by the oculomotor mechanism rather than to the fundamental rules in nature.
        The fundamental rule is that when you move an observational frame of reference, whether it is a ruler, a thumbnail or a stick, away from your eye and toward an object, the object will appear larger; and when you move that reference frame away from an object and toward your eye, the object will appear smaller. More importantly, this rule exists in nature which is beyond our subjective control and of course beyond our oculomotor control. This rule has nothing to do with our knowledge, subjective experience, interpretation, unconscious inference, cognitive interference, and so forth. We have already known and proven this rule by performing the exercise above and the Hering's maneuver. Next we have to explain the rule, i.e., why it exists and how it works.
        First, we have to familiarize ourselves with a new concept called the converging point, as shown in the diagram on the left below. When we look at an object with left and right eyes, one eye has slightly different viewing field from the other. In the diagram, L1 and L2 are two edges of the viewing field for the left eye, and L1 is the right edge line of the viewing field and L2 is the left edge line of the viewing field. Likewise, R1 is the left edge line of the viewing field for the right eye and R2 is the right edge line of the viewing field. As seen in the diagram, only are the left edge line R1 of the right eye and the right edge line L1 crossing each other, and the point where these two lines are crossing each other is the converging point. Between the extensions of these two lines, R1 and L1, is the sub-visual field (vs. the general visual field. See the previous article for details), which is formed when we converge our both eyes or focus on the object. The converging point determines the sub-visual field, but the general visual field still operates in the background unaffected by the sub-visual field. This is why we still can see other objects when we focus on one particular object.

                

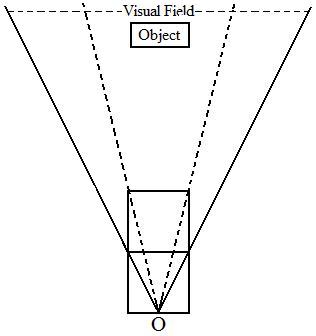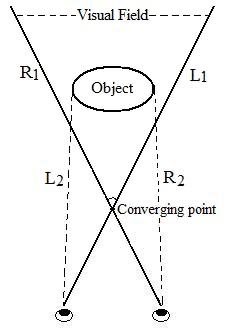
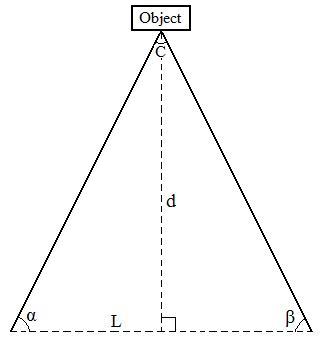
        This concept of converging point is new because it is quite different from the conventional understanding of the angle of convergence, which is the angle C in the diagram on the right above. Pr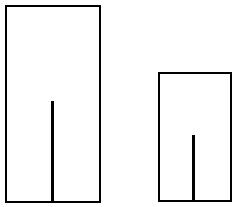obably we all agree that we can focus on an object. But I would like to challenge the conventional understanding of how we focus on objects. This has serious consequence as to understanding the fore-mentioned rule. If we formed a convergence angle on the object when we focus our eyes on it, then we would not be able to see the whole object; rather we could only see a small part or merely a point of the object. This result is incredible. In addition, the convergence angle is used mainly as the distance cue. That is, the convergence angle is larger when you focus on a nearby object and becomes smaller when you focus on a farther away object. The expanding convergence angle plus accommodation of the eyes will give us cues that the object we focus our eyes on is moving closer to us. However, the study by Rock and Ebenholtz in 1959 shows that as long as the central line's proportion in the rectangle (see the figure on the right) is kept the same, we cannot tell whether the rectangle is getting closer or not. My own suggested exercise also shows the same result (see the previous article for details). That is, holding a photo in your hand and focusing on the photo only, you do not perceive the objects or people in the photo becoming larger or smaller while moving it closer or farther away. As a result of these two experiments, the convergence angle and accommodation of eyes can be dismissed as cues to distance; more importantly, the convergence angle may not exist at all. On the other hand, the converging point is more likely to be there to help us to focus on objects.



        Let's look at the converging point in the diagram above again. This time we pay more attention to the angle above the converging point, which can be called the converging angle. But the converging angle is qualitatively different from the angle of convergence discussed earlier. First of all, the converging angle does not provide information about distance of the objects we focus on, because the converging point is always some distance away from the objects. Secondly, the converging angle does not determine the perceived size of the objects we focus on. Even though the converging angle would be larger when we focus on a closer object than a farther object of the same size, it is most likely that we do not perceive the converging angle at all; thus this converging angle change would not affect our size perception. The perceived size of objects is determined by the visual field volume as shown in the equation Ps = S / v. The diagram below illustrates our experience of viewing objects through tubes, which provides further evidence for the conclusion: the perceived size of objects is determined by the visual field volume. The object looks smaller when viewing it through two tubes than when viewing through only one tube. As shown in the diagram below, as the converging point is fixed at O, the visual field represented by two solid lines spreading out from the converging point is much larger than that represented by the dotted lines. As such, the visual field volume is smaller for the viewed object, so it looks larger. 


        Although the converging angle cannot tell us much about the distance and objects' size, it is still very important to understand it. It is quite possible that the converging angle has a maximum angle and a minimum angle. When we focus on an object that is approaching us, the converging angle is increasing. But, the converging angle will not increase anymore as long as it reaches its maximum degree. This is probably the reason why we cannot focus on an object that gets too close to our eyes because the object has passed the maximum converging angle. Also, we know that we cannot focus on an object beyond certain distance, which is set as 10 meters by the perception researchers. I think the limitation of focusing on a far object is caused by the minimum converging angle. That is, the converging point cannot be moved forwards anymore when the minimum converging angle has been reached. At this point, an object that moves further away will be out of focus. However, I think that the limitation of 10 m is probably set for focusing on average human being. How far we can place the converging point depends on the size of the objects we are focusing on. For a small object such as an ant the minimum converging angle can be reached at a very close distance; thus we can hardly focus on an ant at 1m, let alone 10 m. In contrast, for a large object such as a large building or mountain the minimum converging angle will be reached at a very long distance; therefore we can focus on them well beyond 10 m.
        If our eyes can focus on an object and bring the converging point close to the object, the sub-visual field volume will be small enough for the object to occupy a large portion of it. And if our eyes can focus on an object that is moving away from us and keep the converging point at approximately the same distance to the object, the sub-visual field volume will be approximately the same around the object so that it will appear to be about the same in size even though the distance between the object and the eyes is increasing. As a result, size constancy is achieved without taking into account, calculating, computing, compensating, top-down processing, and so on. All we need to do to have size constancy is to focus on the object. The nature has its way to keep things simple and effective, which is why the rule of parsimony is applicable in most cases. Now hold up your hand and focus on it all the time when you move the hand close to and away from your eyes. The hand does not seem to change size at all. If you look at somebody's hand of the same size from 10 m away, the hand appears to be much smaller than yours. It is because that hand is beyond the minimum converging angle of your focus; thus the sub-visual field volume becomes quite large for that faraway hand.
        By the way, experiments have shown that even when one eye is covered, or blind, the muscles and the eye lens still accommodate to the distance perceived by visual information supplied by the other eye. Also, when the eye lens muscle is paralyzed in both eyes by use of atropine drops, micropsia still occurs. It seems that micropsia are not the  result of physical changes in the eyes, but are caused by processes occurring in the brain, the same processes that control the muscles of the eyes and the ciliary body that adjusts the focus of the eye lens. However, I have a different explanation for why micropsia occurs, which I will discuss next. But, based on these studies it suffices to say that we will have the same converging point and converging angle even though we are viewing objects with only one eye.


TOP

Back to the Ames Room Index
 

References

     Kaufman, L. & Rock, I. (1962). The moon illusion I. Science, 136, 1023-1031.
     Broerse J. et al. (1992). The apparent shape of afterimages in the Ames room. Perception, 21(2): 261-8.


Related Information on the Web:

http://en.wikipedia.org/wiki/Ames_room
http://www.psychologie.tu-dresden.de/i1/kaw/diverses%20Material/www.illusionworks.com/html/ames_room.html
http://psychology.about.com/od/sensationandperception/ig/Optical-Illusions/Ames-Room-Illusion.htm
 http://www.newworldencyclopedia.org/entry/Ames_room

Appendix A: The Perceived Size and Its Mathematical Equations




<< Previous    Home    Next >>