The Perceived Size (Ps) and Visual Field Volume

        We usually do not perceive the same object as getting smaller or shrinking when it recedes from us; for instance, you don't perceive your hand as becoming smaller when you extend your arm to move it further away from your eyes. "It is a well-known fact that the apparent size of an object depends not only on the size of the retinal image or visual angle but on the distance as well. Within certain limits, objects do not appear to vary substantially in size when viewed from varying distances, despite the fact that the size of the optical image varies inversely with distance. This phenomenon is known as size constancy. It is as if the observer took the distance into account in perceiving the size of the object " (Kaufman & Rock, 1962, p.953). As quoted above, Kaufman and Rock summed up this phenomenon very well. Now we can use the equation S = θ · D (which is derived from the equation: θ = S / D) to further explain the phenomenon of size constancy. In this phenomenon the size of an object, S, stays constant or unchanging even though the retinal size θ is changing with the distance D. In order to keep the size of an object, S, constant, our brain has to take the increased distance D into account when the retinal size θ is becoming smaller or to take the decreased D into account when the retinal size θ is getting larger. In other words, our brain has to compensate the changed θ with equal proportion of changed distance to balance the equation S = θ · D.
        The Ames Room illusion supposedly shows us that the peculiar shape of the room which supposedly removes all distance cues and does not allow for proper scaling of object size would cause us to lose our ability to maintain size constancy. If we use the same equation S = θ · D again, we will gain a better understanding of the illusion. For the viewers of the Ames Room the distance D in the equation is the same from one end of the room to the other end. When an individual walks from the near corner to the far corner, the retinal image size θ of that person is, however, decreasing with distance. Since D is the same value, the individual's size S cannot be compensated with different D and hence cannot be maintained so that we see people or objects as the same size as their retinal images. By and large the Ames Room illusion can be expressed by S = θ because the constant D can be eliminated from the equation S = θ · D. The Ames Room illusion supposedly tells us that it is essential to have adequate distance cues and proper estimate of distance from objects; otherwise we would have very strange size perception if we were fooled by a distorted room regarding the distance from the objects. All in all, the perceived distance of objects is supposed to be very important for us to have proper size perception.
        However, the size (or linear size) of an object S and the visual angle θ are supposed to be qualitatively different concepts. The S is supposed to be a size close to the actual size of the object and the θ is supposed to be a size close to the retinal image; therefore, they cannot equal each other. The visual angle θ can represent an infinitely small object when it is very close to the vertex and also represent an infinitely large object when it is very far away. In fact, the θ does not represent any particular object with a fixed size at all. We certainly cannot perceive the θ on the retina because it would not register on the retina. It can only be measured by a measuring equipment such as a theodolite or behaviorally by pointing gestures. From the example of looking at a faraway house through a nearby window given in the earlier section we can assume that the linear size S is the approximation of the actual size of objects and the visual angle θ is the approximation of the retinal image size.
        Professor Kaufman suggested a practical way to distinguish S from θ: If a subject matches a length in meters of a distant rod to that of a nearby rod, as in a size constancy experiment, we refer to perceived linear size; if a subject adjusts the length of a nearby rod so that it subtends the same angle at the eye as a distant rod, we refer to perceived angular size. Thus, the linear size is an approximate measurement of the objects' physical size and the angular size is an approximate measurement of the retinal size of the objects. Now let's use a ruler to measure an object. If we place the ruler against the object, the measurement is the linear size of the object; if we place the ruler very close to our eye, the measurement is the angular size of the object, representing the retinal size. Assume that the distance between the object and our eye is 100 units. When we put the ruler at 100 units from our eye and on the object, we are measuring the linear size of the object. When we put the ruler at 1 unit from our eye which presumably happens to be θ radians, then we are measuring the angular size or retinal size. What if we put the ruler at units between 2 and 99, what kind of size are we measuring? To further illustrate my point, let's do an exercise: Turn on a TV set of unknown distance and size; cut a hole in a piece of paper and make that hole the same shape as the TV set. According to the conventional definitions, when we put the paper against the TV set and cut a hole as large as the TV set, we know the hole represents the linear size of the TV set; when we put the paper very close to our eye and cut a hole just big enough to fit the image of the TV set, we know the hole represents the retinal size of the TV set. What if we put the paper somewhere in between and cut a hole that just fits the image of the TV set? Since we do not know the actual size and distance of the TV set, we could easily assume that we are placing the paper against the TV set so that we are looking at the linear size of the TV set. Then again, the image we are looking at is by definition not the linear size or the angular size of the TV set; therefore, we are in a definitional limbo.
        The terms of linear size and angular size are very confusing and inaccurate, and they both refer to the perceived size of objects. As such, it is time for us to have a new understanding of the perceived size. The visual angle θ should be abandoned in this new understanding because it is an abstract mathematical idea invented to describe the relationship between object's size and distance. It does not exist in reality and of course we cannot perceive it. As a matter of fact, in the equation θ = S / D, θ is the calculated result of S / D and θ depends on S. Thus, θ changes only when S changes, not the other way around as suggested in the Ames Room illusion, that is, S changes with θ with D unchanging. Consequently, the perceived size of an individual should not change at all in the Ames Room no matter where he or she is in the room. The reason is that D is perceived as the same based on the shape of the room and S should be perceived as the same as well based on our knowledge that a person does not change size instantly, which is called identity constancy. So our conventional understanding of the perceived size based on this equation has to be modified.
        I have discovered a new term, Ps, and its equation which can explain the size perception is, I believe, much better than the conventional equation θ = S / D (see Appendix A for details). For the two dimensional measurement the equation is expressed as: Ps = S / d² (Appendix A). But in the conventional discussion of the size perception, S always stands for one dimensional measurement such as height for square or rectangular shapes and diameter for spheres. To follow suit of the convention, the equation can be written as: Ps = S / d,  where Ps is the perceived size of the object; S is the height or diameter of the object; and d is the distance between the observer and the object. The new equation Ps = S / d looks pretty much like the old equation θ = S / D; but these two equations are fundamentally different. Unlike θ in the equation θ = S / D which could represent something ranging tremendously in size, the perceived size Ps represents a specific object with fixed size. And unlike S in the equation θ = S / D which is indeterminate as shown by the Ames Room illusion, S in this new equation is quite definite and it represents the actual size of an object, even in the Ames Room.
        By my own definition, Ps is the actual size of an object, S, at a distance d measured at 1 unit away from the viewing eye. Accordingly, the perceived size Ps represents the actual object at a distance whereas the visual angle θ is a mathematical calculation of the actual object which may not correspond to the actual object when the depth information is unavailable or disguised as in the Ames Room illusion. At this point, someone might protest that Ps is measured at 1 unit from the eye, so it is very close to the eye and could be the equivalent of θ. However, Ps does not have to be measured at 1 unit. It can be measured at 2 and more units from the eye and Ps will increase proportionally as the measuring instrument such as a ruler moves away from the eye and toward the object. When we place the ruler against the object, Ps = S because now we are perceiving the object at no distance by means of a ruler. However, we cannot perceive the actual object itself. The reason is that we cannot see the whole object if we place our eye at the same position as the object. Thus, we can only perceive the sizes of objects indirectly through an instrument at a distance. When we say Ps = S at no distance, we do not perceive S directly and S is actually Ps (see Appendix A for details).
        From the viewpoint of the new equation, in the Ames Room it is the perceived size of an individual that is getting smaller, not the angular size, when he or she moves from the near corner to the far corner. To fully understand this statement, we need to look at an example as shown in the picture below. The author of the picture thinks that he has created the Ames Room size illusion without the room when he has moved the background figure to the same elevation as the foreground figure. His reasoning goes like this: In the Ames Room, the person appears to travel along an apparently horizontal and level surface where there is no observed rise in relation to the horizon as the figure recedes; but on a level surface as someone recedes into the distance the level of their feet rise and the level of their head lowers in relation to a true horizontal line. Thus, the picture shows that the figure in the background whose feet are at a higher elevation appears perfectly normal in comparison to the foreground figure even though its visual angle is much smaller, and illusion occurs when the feet of the smaller figure have the same elevation as the bigger foreground figure. However, the illusion in this picture is quite different from the Ames Room illusion; it is a variant of the Ponzo illusion instead. If we use the old equation S = θ · D, in the picture below the angular size θ is the same for both the background and foreground small figures; as a result, the perceived linear size S increases or decreases as the distance D increases or decreases in order to keep the equation balanced. On the other hand, as discussed earlier, the Ames Room illusion shows that S changes with θ when D is the same. What the Ames Room attempts to do is to limit the depth information so that the angular size θ determines what we see, whereas the picture below makes an effort to limit the information about the angular size θ so that the distance D determines how big the objects appear to be.     

        Now look at the picture on the left below, which is the same picture as the one above. The difference is that I have moved the background figure to the side rather than to the foreground. The newly moved figure is at about the same elevation as the background figure. However, the small figure on the side appears to be smaller than the background figure even though they are at about the same distance from the viewer. I have anticipated this result based on my understanding of the Delboeuf and Ebbinghaus illusions. The background figure is enclosed by the smaller arches, especially the small arched opening at the back, and the side small figure is enclosed by much large arch over his head. This outcome is determined by the principle: The smaller portion of the visual field an object occupies, the smaller the object appears to be, and vice versa. To move the background figure to the side is like moving the central circle from the right position to the left position as shown in the modified Ebbinghaus illusion figure on the right below.

                    

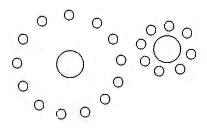
         The diagram below shows two small vertical lines of same height in the room. But in comparison the left vertical line occupies a smaller portion of the back wall than the right vertical line. I think that this difference is the key to the Ames Room illusion, not the distorted depth perception as believed by all the Ames Room researchers. If we make the room cubic and keep the back wall slanted, that is, one side is taller than the other side, the illusion that a person appears to get smaller as he or she walks from the shorter end to the taller end of the back wall will still occur. The illusory effect of this modified Ames Room is like moving the central circle in the above Ebbinghaus illusion figure to larger and even larger surrounding contexts. In this case the distance is not necessary for the illusion. Now let's look at the old equation S = θ · D again. When the room is cubic, meaning that the distance D to the viewer from one end of the back wall to the other end is exactly the same, the angular size θ will stay the same because the person walking along the back wall will presumably cast the same sized retinal image. Strangely, the perceived linear size S is changing even though θ and D on the other side of the equation are remaining the same. Now we have a serious problem of balancing the equation. This result can nearly deal a fatal blow to the old equation and understanding of the size perception. It is why Don McCready has to propose the perceived (or subjective) values for the variables to replace the old equation, i.e., S' = θ′ · D'. In so doing, we don't have to worry about θ′ and D' staying the same in the Ebbinghaus illusion or the modified Ames Room because they can be changed subjectively, either by way of our experience and interpretation or by way of unconscious inference. In other words, there is no need for objective properties in the equation S' = θ′ · D'; the variables can be changed at will to keep the equation balanced.  

        Unfortunately, there is a momentous problem associated with McCready' new equation. If the distance D' and the linear size of an object, S', are subjective, then it means that they are changeable and could be quite different from individual to individual. As such, one person's retinal image θ′ would be quite different from another person's. This is really a peculiar consequence of the proposed equation. My equation Ps = S / d tells us that the perceived size of an object at certain distance is always the same for all human beings. Hence the proposed equation by McCready is incredible.
        As shown by the Ebbinghaus illusion and the modified Ames Room, the distance has played no role in the illusion. If we measure the central circles in the Ebbinghaus illusion at the same distance with the same units from our eye, the perceived size is the same for both circles. This is a unique circumstance under which we only focus on the specific objects measured and the ruler has limited the visual field volume to the same degree for both circles, which will be discussed next. But, we know that the perceived size of the central circles have changed when they are placed in a surrounding context representing different sub-visual field volumes with the distance d remaining the same. And we know that the actual size of an object, S, does not change instantly. Somehow the perceived size Ps changes when the object is placed in the different surroundings. It only means that there is something else besides the distance which plays a crucial role in causing Ps to change. This factor has a much more fundamental influence on our size perception than the distance. This factor is the visual field volume v, as discussed in the previous article, which can replace the distance d in the equation Ps = S / d; therefore, the new equation for perspective, the Delboeuf and Ebbinghaus illusions etc. is expressed as follows: Ps = S / v. Accordingly, the perceived size Ps of the individual who walks from the shorter end of the back wall to the taller end will reduce because the visual field volume of the taller wall is larger which is inversely proportional to the perceived size Ps. The reason why the distance d can be replaced by the visual field volume v is that the distance can be derived from the visual field volume, not the other way around (which was discussed in the previous article). Therefore, the visual field volume is more fundamental than the distance in affecting the size perception. For instance, in the Ames Room illusion the distance cues are lacking regarding the further distance of the far corner of the room; but we still perceive the figure in the far corner as smaller. If the perceived distance is the determining factor, the object would be perceived to be the same no matter where it is along the back wall.

         The photograph below taken by English visual psychologist Richard Gregory shows two people, placed at differing distances, so that their images differ in size just as in the Ames Room. Most people looking at this photograph stated that the nearer person looks a little nearer, but also a lot larger. The two subjects maintained a constant horizontal foot level independent of their distance from the viewer (this was accomplished by having the camera placed at ground level). In a normal situation, the smaller figure should be on a higher level in the visual plane than the larger and closer figure and a perspective background would also be present. In sum, the Ames Room inspired photo below attempts to show that we fail to perceive objects' or people's sizes accurately when all the cues to distance are removed; instead, we have to rely on the retinal image for our size perception. Worst of all, the visual field volume seems to be the same for the two women in the photo. Subsequently, how could we use the equation Ps = S / v to explain the phenomenon in this photograph? This is the issue with which I am going to deal in the next section.