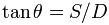The diagram above illustrates an observer's eye looking at a frontal extent AB that has a linear size S (also called its "metric size" or "tape-measure size"). The extent's lower endpoint at B lies at a distance D from point O, which for present purposes can represent the center of the eye's entrance pupil. The line from B through O indicates the chief ray of the bundle of light rays that form the optical image of B on the retina at point b, i.e., on the fovea. Likewise, endpoint A is imaged at point a. The visual angle θ is the angle between the chief rays for A and B. The visual angle θ can be measured directly using a theodolite placed at point O. Or, it can be calculated using the formula, θ = 2arctan(S / 2D). However, for visual angles smaller than about 10 degrees, this simpler formula provides very close approximations: 

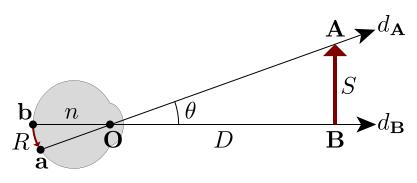
The retinal images at b and a are separated by the distance R, given by the equation:

in which n is the eye's nodal distance that averages about 17 mm. That is, a viewed object's retinal image size is approximately given by R = 17 S/D mm or R = 17 θ mm. The line from point O outward through object point B specifies the optical direction, d_B, of the object's base from the eye, which is directed toward the horizon. The line from point O through point A specifies that endpoint's optical direction, d_A, toward some specific elevation value (say, 18 degrees). The difference between those real directions (d_A - d_B) is, again, the visual angle θ. Also, the visual angle θ is the perceptual correlate of the "size" of the retinal separation R mm, or it is approximately the equivalent of the retinal image size. In other words, we cay say that θ is mediated by the retinal image size R mm or the retinal image R mm is directly valuated (or scaled) by θ.

        The diagram above illustrates the perceived (subjective) values for a viewed object. Point O′ represents the place from which the observer feels that he or she is viewing the world; D′ is the perceived distance of the subjective point B′ from O′. The observer might simply say how far away point B′ looks, in inches or meters or miles. Similarly, S′ is the perceived linear extent by which the subjective point A′ appears directly above point B′. The observer could simply say how many inches or meters that vertical distance looks. For a viewed object, S′ thus is its perceived linear size in meters, (or apparent linear size). The perceived endpoint at B′ has the perceived direction, d′_B, and the observer might simply say "it looks straight ahead and toward the horizon." The object's other perceived endpoint, A′, has a perceived direction d′_A, about which the observer might say "it appears toward a higher elevation than point B′." The difference between the two perceived directions (d′_A - d′_B) is the perceived visual angle θ′, also called the perceived angular size or apparent angular size.
        It is, however, deemed to be very hard to quantify θ′. For instance, some observers might say that point A′ "looks about 25 degrees higher" than B′, but most of us cannot reliably say how large a direction difference looks. We often rely on pointing gestures to suggest the perceived visual angle; for instance, we often tell someone about the change in the directions we see for two viewed points by pointing something, e.g., a finger or our eyes from one point to the other. Therefore, in some experiments the observers aimed a pointer from one viewed point to the other; so the angle through which the pointer rotated was the measure of θ′. Also, because θ′ specifies the amount by which one should rotate one's eye to quickly look from one seen point to another eye tracking, observers in other experiments shifted their gaze from one object endpoint to the other, and the angle the eye rotated through was measured as θ′ for that object.
        It is believed to be important to understand how θ′ differs from S′. An example is illustrated by the sketch on the right. Suppose we are looking through a window at a 30-foot-wide (9.1 m) house 240 feet away, so it subtends a visual angle of about 7 degrees. The 30-inch-wide (760 mm) window opening is 10 feet away, so it subtends a visual angle of 14 degrees. We can say the house "looks larger and farther away" than the window, meaning that the perceived linear size S′ for the house's width is much larger than S′ for the window; for instance a person might say the house "looks about 40 feet wide" and the window "looks about 3 feet wide." We also can say the house "looks smaller and farther away" than the window, and that does not contradict the other statement because now we mean that the amount (θ′) by which directions of the house's edges appear to differ is, for instance, about half the apparent direction difference for the window edges. As such, we experience both the linear size and the angular size comparisons at the same time, along with the distance comparison. Thus any report that states merely that one object "looks larger" than another object is considered to be ambiguous. It is required to specify whether "looks larger" refers to the perceived angular size (θ′) or to the perceived linear size (S′) or to both of those qualitatively different "size" experiences. It is believed that in everyday conversations "looks larger" often refers to an angular size comparison rather than a linear size comparison.

        How the three perceived values θ′, S′, and D′ would be expected to relate to each other for a given object is illustrated by the diagram above and stated by the following equation, which is dubbed by some as the "perceptual size-distance invariance hypothesis": 
or simply θ′ = S' / D'. Conventional "textbook" theories of "size" and distance perception do not refer to the perceived visual angle and some researchers even deny that it exists. This idea that one does not see the different directions in which objects lie from oneself is a basis of the so-called "size-distance invariance hypothesis" (SDIH). That old SDIH logic (geometry) is typically illustrated using a diagram that resembles the diagram above, but has the physical visual angle θ substituted for the perceived visual angle θ′. The equation for the SDIH thus is

Here, S′ is typically called the "perceived size" or "apparent size"; more precisely it is the perceived linear size, measured in meters. When rearranged as S′ = D′·θ, the equation expresses Emmert's law (which will be discussed in the next article).
        The perceived visual angle has been used to explain the Ebbinghaus illusion, for instance. In the Ebbinghaus illusion figure on the right, the two central circles are the same linear size S and the same viewing distance D; so they subtend the same visual angle θ and form equal-sized retinal images (see the previous article for details). But the right central circle "looks larger" than the left one. According to the SDIH, "looks larger" can mean only that S′ is greater, and with the physical angle θ the same for both, the SDIH requires that D′ be greater for the right circl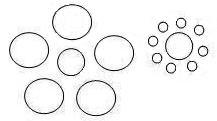e than for the left one. However, for most observers, both circles appear unequal while also appearing at the same distance (on the same page). This commonly found disagreement between published data and the SDIH is known as the "size-distance paradox". The "paradox" completely vanishes, according to McCready, when the illusion is described, instead, as basically a visual angle illusion: that is, the perceived visual angle θ′ is larger for the right central circle than for the left central circle. It is as if its retinal image were larger. So, according to the "new" perceptual invariance hypothesis (θ′ = S′/D′), with θ′ larger for the right circle, and with D′ correctly the same for both circles, then S′ becomes larger for the right one by the same ratio that θ′ is larger. As a consequence, the right central circle looks a larger linear size on the page is because it looks a larger angular size than the left one.
        As already introduced, the magnitude of an object's visual angle θ is believed to determine the size R of its retinal image. In turn, the size of the retinal image is believed to determine the extent of the neural activity pattern the retina's neural activity eventually generates in the primary visual cortex, area V1 or Brodmann area 17. This cortical area is thought to harbor a distorted but spatially isomorphic "map" of the retina, which has presumably been confirmed by Murray, Boyaci, & Kersten (2006) using functional magnetic resonance imaging.