The main
explanation of the Ebbinghaus illusion is the size contrast or visual
angle contrast theory.
It states that the perceived size of an object is influenced by its
contrast with nearby contextual objects. If the objects in the nearby
surrounding context are smaller in contrast, the viewed object is
perceived as larger than those without the context; and if the objects
in the nearby surroundings are bigger in contrast, the object is perceived as smaller. There are two suggested ways for this contrast to happen:
One is the simultaneous contrast in which the changes occur when you
look at the target object and the size of the visual angles subtended
by extents that appear close to the target object;
another is the successive contrast in which the changes occur when you
first intently stare at the extents of nearby objects and then view the
target object. Another popular explanation for the Ebbinghaus illusion
is that the illusion is caused by linear perspective, that is, the larger surrounding circle looks closer than the smaller surrounding one; therefore, the solid black circle that looks farther away is interpreted as bigger because a far object has to be bigger in actual size for it to have the same retinal image size as a near object. This
phenomenon is also explained by the "size constancy theory" or "taking
into account hypothesis", that is, our brain takes the distance into
account when interpreting the retinal image information; thus,
a longer distance will make the perceived size of an equal retinal
image larger. I am going to challenge all of these hypotheses and theories in this article.
My explanation of the Delboeuf illusion and many other related illusions is brand new and has never been explored by anyone else. To understand my explanation of the illusion it is necessary to first understand one important concept, the visual field. The visual field is the angular or linear extent of the observable world that is seen at any given moment. Your visual field covers a fixed angle and has a conical shape. As you look farther away, this cone spreads out to cover a wider area of view. But this area still has to be focused onto the same-size retina, so obviously the image of a given object will take up proportionally less of your retina if it is 100 meters away than if it is 10 meters away. A way to envision this conical visual field is the beam of light extending from a flashlight. As you get farther away from the beam of flashlight, the width of the beam gets larger; likewise, your eyes can see a greater width when looking at things farther away. Now look at the figure on the left below. The objects A and B are identical in size, and O is the observer. The closer object B covers a larger portion of the visual field than the object A which is farther away from the observer. To test this, hold a book in your hand. When you hold the book very close to your eyes, the vision cone may not even cover an entire page. When farther away, the book will only fill a small part of your vision cone. When very far away, the book covers such a small portion of the vision cone that you may not even notice the book is there because you see more at a distance and each object becomes a smaller portion of all that you see. This is the main reason why objects appear larger when they are closer to us and smaller when far away. The second reason is illustrated in the figure on the right below, in which the closer object B occludes twice as many small black circles as the same-sized A which is farther away. Thus, as an object moves closer to us, it occludes more contextual objects than a faraway object of the same size. This is why the relationship between distance and apparent size of objects is considered by many psychologists as being not a linear pattern. If an object were actually touching the eye, thus being at no distance at all, it would appear infinitely tall. James Gibson suggests that the perceived-size constancy can be explained by the unvarying size ratio of objects in a scene without having to refer to distance at all. The example given for this suggestion is a man standing next to a house. His height bears a definite size relation to the height of the house. That relation will not change, no matter from how far away we view the man. Gibson's idea of perceiving size without relying on distance is consistent with my own. However, his size ratio concept is incorrect in the real world. His example works in a 2-D picture or photograph in which the relative size of the man in contrast to the house is unchanging no matter where you view the picture. Conversely, in the real 3-D world, as shown in the figure on the right below, as we move closer to the man, he will occlude a larger proportion of the house and eventually block the house entirely when we get really close to him. As such, the perceived size of objects is not only determined by their proportion in the visual field, though it is the most important factor, but also determined by how much background objects they occlude.
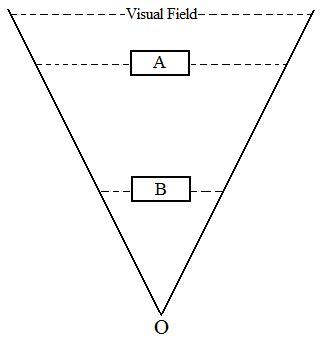
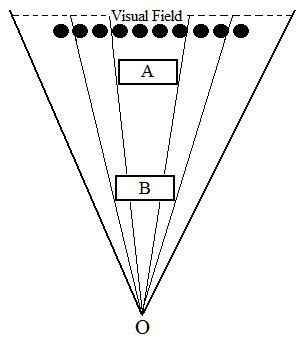
My explanation of the Delboeuf illusion and many other related illusions is brand new and has never been explored by anyone else. To understand my explanation of the illusion it is necessary to first understand one important concept, the visual field. The visual field is the angular or linear extent of the observable world that is seen at any given moment. Your visual field covers a fixed angle and has a conical shape. As you look farther away, this cone spreads out to cover a wider area of view. But this area still has to be focused onto the same-size retina, so obviously the image of a given object will take up proportionally less of your retina if it is 100 meters away than if it is 10 meters away. A way to envision this conical visual field is the beam of light extending from a flashlight. As you get farther away from the beam of flashlight, the width of the beam gets larger; likewise, your eyes can see a greater width when looking at things farther away. Now look at the figure on the left below. The objects A and B are identical in size, and O is the observer. The closer object B covers a larger portion of the visual field than the object A which is farther away from the observer. To test this, hold a book in your hand. When you hold the book very close to your eyes, the vision cone may not even cover an entire page. When farther away, the book will only fill a small part of your vision cone. When very far away, the book covers such a small portion of the vision cone that you may not even notice the book is there because you see more at a distance and each object becomes a smaller portion of all that you see. This is the main reason why objects appear larger when they are closer to us and smaller when far away. The second reason is illustrated in the figure on the right below, in which the closer object B occludes twice as many small black circles as the same-sized A which is farther away. Thus, as an object moves closer to us, it occludes more contextual objects than a faraway object of the same size. This is why the relationship between distance and apparent size of objects is considered by many psychologists as being not a linear pattern. If an object were actually touching the eye, thus being at no distance at all, it would appear infinitely tall. James Gibson suggests that the perceived-size constancy can be explained by the unvarying size ratio of objects in a scene without having to refer to distance at all. The example given for this suggestion is a man standing next to a house. His height bears a definite size relation to the height of the house. That relation will not change, no matter from how far away we view the man. Gibson's idea of perceiving size without relying on distance is consistent with my own. However, his size ratio concept is incorrect in the real world. His example works in a 2-D picture or photograph in which the relative size of the man in contrast to the house is unchanging no matter where you view the picture. Conversely, in the real 3-D world, as shown in the figure on the right below, as we move closer to the man, he will occlude a larger proportion of the house and eventually block the house entirely when we get really close to him. As such, the perceived size of objects is not only determined by their proportion in the visual field, though it is the most important factor, but also determined by how much background objects they occlude.


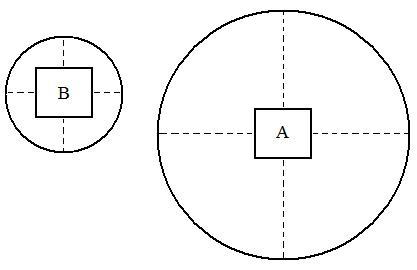
The above two
figures are in fact the top view of the objects in the visual field.
They merely depict a one-dimensional view of the visual field. The
width of the visual field depicted in the figures is in fact the
diameter of the
actual conical visual field. If we look at the visual field from the
point of view of the actual observer rather than the view from the top
of the visual field, what we will actually see is shown in the figure
below. The objects A and B are square-shaped rather than the rectangles
viewed from the top. The conical visual field has two dimensions, its
width and height. In the figure below we are seeing something similar
to the Delboeuf illusion. Although the squares A and B are identical in
size, the square A looks smaller than B because A occupies a smaller
portion of the visual field in comparison to B. The perceived size of
an object is inversely proportional to the visual field volume, which
is determined by this equation: Ps = S / V (where Ps is the perceived size of an object; S is the actual size of the object; and V is the visual field volume). This is the principle we are going to use to explain all the other illusions in this article, i.e., The
smaller portion of the visual field an object occupies, the smaller the object appears to be, and vice versa.