


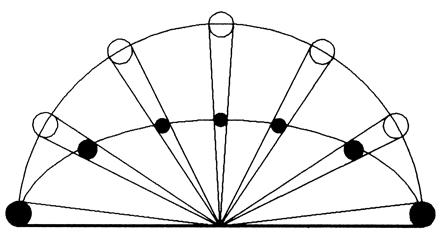
The second theory is the apparent distance theory which is the older of the two theories and is more popular. As a matter of fact, the apparent distance theory is more often than not the explanation for the Moon illusion in the textbooks. Basically, the theory holds that the perceived distance to the moon at the horizon is greater than that to the zenith moon. The figure below shows how the horizon moon's greater perceived distance could cause it to be perceived as larger. As shown in the figure below, regardless of its elevation, the distance between an observer (at the center of the horizontal line) and the moon remains constant (unfilled circles). However, a moon perceived as growing closer as its elevation increases (filled circles), must appear as growing smaller. This figure illustrates a version of the theory in which the perceived size of the moon is proportional to its perceived distance, a relationship known as Emmert's law.
Since we have already discussed Emmert's law in the last article, let's
spend some time on this version of the theory,
i.e., Emmert's law and the apparent distance theory. As far as the
proportional relationship between the perceived size of objects and the
perceived distance is concerned, it has been already refuted
effectively in the last article. There is no need to discuss that again. I am going to critique this version of the theory from another perspective.
I think that the constant retinal size of the afterimages and the moons
of various elevations is the starting point for the apparent distance
theorists to use Emmert's law to explain the Moon illusion. They
believe that the afterimage is burnt onto the retina temporarily, just
like an image on the film.
There is no way for the retinal afterimage to change size unless our
brain intervenes to alter the perceived size in the visual cortex.
The projected afterimage on a surface is not the projection of the
retinal image itself, but the outcome of the brain's intervention. What
happens is that our brain uses all kinds of distance cues to figure out
the distance between the surface and our eye and then uses the
perceived distance to "magnify" the retinal afterimage in the visual
cortex, so we can perceive a larger afterimage on a farther surface. If this is true, then the figure above will make sense.
The actual distance of the moons of various elevations becomes
irrelevant. Since the retinal afterimage size is constant, all our
brain needs is the information about the distance in order to ensure
the consistency of perceived size and distance.
If our brain believes the sky is shaped like a dome represented by the
curved line connecting the filled circles, the perceived size of the
moons should correspond to the relative distances as shown by the
filled circles in the figure above.
However,
I have found out that the projected afterimages are not in the brain
only, they are real projections in the outside world, like movies
projected onto a screen by a movie projector, though it sounds very
strange (see the last article for details).
The proof is that we have to converge our eyes physically on the far
projection to perceive the larger afterimage and we cannot do so
through a tube. If our brain simply makes use of the distance
information to amplify the constant retinal image, then the tube should
not be able to prevent it from doing so. Somebody might protest that the tube could obscure many distance cues to make the distance more indeterminate.
I would say that you can include as many distance cues as possible
within the view field of the tube, and results will always be the same,
that is, the distance has no effect on the perceived afterimages at all.
The afterimages are always perceived to be the same size while viewing
through a tube no matter where the projections are. If the perceived
moon size is indeed similar to the projected afterimage, it does not
matter whether the moons are at the positions of the filled circles,
unfilled circles, or even further away because they will be perceived
as the same no matter how faraway or how close they are from our eye
while viewed through a tube.
As long as the retinal image is constant, the distance between the
moons and the eye is inconsequential. A faraway projection of the
afterimage can be perceived as smaller if viewed through a tube; and a
closer projection of the afterimage can be perceived as larger if
viewed without the tube.
It is a common experience that
the horizon moon and the zenith moon look the same when we view them
through a tube. This constant retinal image size of the moons of
various elevations is also demonstrated by using a ruler, a coin, your
thumb, a telescope, a camera, etc.
For instance, it is suggested to choose a coin of certain size to match
the size of the horizon moon at extended arm position and then to cover
the zenith moon with the same coin at the same position;
you will find that the both moons have the same size. Also, a
double-exposure photograph of the horizon moon and the zenith moon
shows
that the two moon images have the same diameter on the film (and a
print) because it is believed that the angle the endpoints of the moon's diameter subtend
at a camera lens remains the same.
All these methods of proving that the horizon moon and the zenith moon
are the same size on our retina have one thing in common, i.e., a fixed
converging point. (Please read The Ames Room Illusion for details.) As long as we can move the converging point closer to the viewed target, it will be perceived as larger.
The fact that the horizon moon is slightly farther away from us is
inconsequential, as said before. That the horizon moon is perceived as
larger is because we can converge our eyes more closely on the horizon
moon than the zenith moon. On the other hand, the conventional interpretations of viewing the horizon moon through a tube are twofold. One is that the "horizon effect" disappears when we look at the horizon moon through
a tube because the tube obscures any familiar reference objects so that
we do not have direct comparison with reference objects of known size
anymore. Another interpretation is that the tube provides a visually
dominating reference object already judged to be "near".
These interpretations on the basis of the size contrast theory have already been refuted earlier and in the previous articles.
All versions of the apparent
distance theory have to deal with the so-called "size-distance paradox".
The paradox is that the larger-looking horizon moon, according to the
apparent distance theory, is due to the longer perceived distance, and
the observers are required to say the horizon moon "looks larger and
farther away";
but for most people the larger-looking horizon moon either looks about
the same distance away as the zenith moon, or, more often than not, it
looks closer than the zenith moon. To resolve this obvious paradox, it is suggested that there are two separate mechanisms at work in the
perception of size and distance. First, our brain generates the apparent distance from various cues to distance available
in the visual scene, including relative size, perspective and image
overlap etc. and then employs the perceived distance to
an object to generate a size percept of the viewed object. Next, our brain does the following logic reasoning: (1) the horizon sky is further away, so the horizon moon
is further away; (2) the further away horizon moon looks larger, which
acts as cue for its apparent distance,
thus the horizon moon looks
nearer. My response to this explanation of two separate mechanisms is
simple. To say it further and also nearer at the same time is against
the laws of thought: A
and not-A, either A or -A. You can perceive A or -A at a time,
but you cannot perceive both A and -A at the same time. If you insist
that you first perceive A (a further distance) and then use the
information from A to deduce -A (a nearer distance), we can
assume that our brain does have such mechanisms and can actually do it.
In so doing, our brain would be very busy with solving such sort of
conflicts just for the Moon illusion alone. For example, apart from looking further and nearer, the horizon moon also looks dimmer because it seems further away and
brighter because it appears nearer. Similarly, the horizon moon looks both blurred and clearer;
both smoother and rougher; both weaker and stronger in gravitational force; both
reachable and unreachable; both colder and warmer; both less and more powerful; and so forth. I think this explanation complicates things even more and it is not parsimonious; therefore it is less possible to be true.
All versions of the apparent
distance theory are based on the notion that the horizon moon is
effectively at a greater perceptual distance than the elevated moon. Apparent
distance theories presume that perceiving the size of the moon involves the same
mechanisms as those involved in perceiving the sizes of ordinary objects.
Accurate perception of an object's size regardless of its distance is referred
to as size constancy. Because the angular size of an object is inversely
proportional to its distance (Euclid's law),
size constancy is possible only if distance is taken into account.
These are conventional understandings of the perceived size and
distance. I have already effectively challenged these positions in the
previous articles.
All I want to say now is simply that the distance between objects and
the eye is inconsequential for size constancy; for instance,
we cannot maintain size constancy of an object (e.g., our moving hand)
while viewing it through a tube or any fixed converging point, even
though we know fully the distance of the object from us. Once we focus
on the object, we do not need to pay attention to the distance and size
constancy will be maintained. In sum, the apparent distance theory is inadequate to explain the Moon illusion.