Home

The Height Illusions

By Grant Ocean

    In psychology, the visual perception is considered to be the ability to interpret visible information reaching the eyes which is then made available for planning and action. To represent the external world in our head, we must detect physical energy from the environment through our senses and encode it as neural signals, a process traditionally called sensation; and we must select, organize, and interpret our sensations in our brain, a process traditionally called perception. Most of time we seem to accurately use our properties of vision to represent the perceptual inputs with little effort. However, failures of perception may occur either during the sensory detection stage or during the perceptual interpretation stage. The above statements are the conventional understanding of our visual perception. But, I am going to challenge them in this article and many more to follow.

    This article and many to follow will focus on one kind of so-called perceptual failures, the static perceptual illusions, which are considered to be systematic distortions of size or shape. But why do they happen? Ancient Greek philosophers had asked the same question about 2500 years ago. They formed two opposing theories to explain the phenomenon of the perceptual illusions: (1) Sensory inputs are variable and inaccurate; the mind is used to correct these inaccuracies and; (2) the senses are inherently accurate and it is the mind that is limited (Coren & Girgus, 1978).

    Recently, theories of perception have been used to explain illusions. While theories of perception can be sorted into categories according to various criteria, based on whether the information processing is required or not (Michaels & other, 1981) we can have two broad categories: the indirect perception theory and the direct perception theory. The indirect perception theory begins with the assumption that the senses are provided with an impoverished description of the world, that is, the input does not provide accurate or complete information about objects and events. Perceptions, however, are comprehended as being very rich, elaborate, and accurate; we know a great number of things about our everyday world. On the assumption of imprecise or equivocal input and the act of meaningful and accurate perceptions, it is then postulated that perception involves a complex set of elaborations upon the input to make it rich. As such, the nervous system provides a variety of additions to its stimulation. From the perspective of the indirect perception theory, illusions are viewed as perceptual errors, or departures from reality (e.g., Gregory, 1997). Perception is the brain's search for the best interpretation of the data that is being presented. Sometimes the "perceptual hypothesis" is incorrect and an illusion results (Gregory, 1997). Thus the perceptual illusions arise from misinterpretation by the brain of sensory information. For the Gestaltists, this suggests that the mind is actively involved in interpreting the perceptual input rather than passively recording the input.

    On the other hand, the direct perception theory states that all information comes to us from our senses and does not need processing from the higher centers of the brain (Michaels & other, 1981; Allard, 2001). Knowledge of the world is thought to be unaided by inference, memories, or representations because stimulation is extraordinarily rich and provides such a precise specification of the environment that a perceiver needs only to detect that information, not elaborate it. The followers of the direct perception theory have criticized the notion of a perceptual hypothesis and hence refused to consider illusions as perceptual errors. Turvey (1996) affirms for instance that, since perception can never be considered erroneous, phenomena such as the so-called size-weight illusion, are in fact not illusions but normal perceptual phenomena that can be explained by the recourse to the right variables the system is sensible to (in the case of the size-weight illusion, the muscular system is sensible to the distribution of the masses of hand-held objects). Turvey’s argument about illusion is about the correspondence between information and perception: If information is picked up, then perception is accurate.

    Early perceptual psychologists understood the philosophical power of illusions. Existing illusions were hotly discussed and the discovery of new illusions was greeted with tremendous fanfare. These simple line figures were thought to be the "windows on the mind." If one could understand the mechanisms of illusions, one would understand the dynamics of perception and perhaps of mind in general. Even though this early hope has not paid off after 150 years of study, many researchers studying the perceptual illusions still believe that it is an effective way to unravel the secrets of our mind. I have pursued the visual illusions with the similar purpose in mind.

       

                                                           

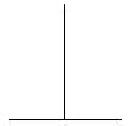
 Vertical-horizontal illusion                                         Top hat illusion                                                          The arc of St. Louis              


    The height illusion is also called the vertical-horizontal illusion, which is the simplest of all the perceptual illusions, and was the first visual illusion to be discovered; and it was discovered by nobody else but the father of experimental psychology, Wilhelm Wundt. The top hat illusion and the famous arc in St. Louis, USA, are considered as variations of the vertical-horizontal illusion since the height of the hat or the arc has the exactly same length as their base, as shown above. Wilhelm Wundt described the vertical-horizontal illusion as the situation where a vertical line looks longer than the horizontal line of equal length, as shown in the figure above. He attributed this distortion to asymmetry of the eye movement system. Although this asymmetry assumption has been invoked many times since to explain distortion illusions, it must be ruled out because the distortions occur in after-images or in normal retinal images optically stabilized so as to remain stationary on the eye. In addition, distortions can occur in several directions at the same time, which could hardly be due to eye movements. For instance, when the standard vertical-horizontal illusion is turned sideways (90°) and on its side as shown in the left figure below, the former vertical line (now the horizontal line) still looks longer.  
              

                                                      

 

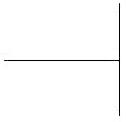
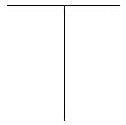
The most acceptable and often-cited explanation for the vertical-horizontal illusion so far is that we perceive objects higher in our field of vision (ground) as farther away and perceive the lower part of a figure-ground illustration (figure) as closer (Vecera & others, 2002; Myers, 2003). Next the Ponzo illusion is used to explain that the closer object is perceived as shorter than the farther away object of the same size because our brain may reason that the farther away object must be longer than the closer object if they have the same retinal images. This explanation is proven unsatisfactory when the so-called figure and ground are turned around as shown in the right figure above. The perception is more or less the same no matter how you rotate the vertical-horizontal figure. On the other hand, using one illusion which is not yet fully understood to explain another illusion is itself problematic. Actually, the vertical-horizontal illusion is most effective when the vertical line is sitting in the middle of the horizontal line as shown in the standard figure. When the vertical line and horizontal line are connected at a right angle by the ends of the lines (see the two figures below), the vertical-horizontal illusion effect of these two figures is diminished extensively, and many observers cannot even tell which line is longer. The different illusory effects between standard and all the other figures tell us that the vertical-horizontal illusion is probably not caused primarily by the different perceptions of the two lines, but something else is playing a role.

                                                          

    Although the vertical-horizontal illusion looks the simplest of all the illusions, it is actually not easy to find a satisfactory explanation for it. Having discredited all the existing explanations, I was at a loss for awhile and didn't know how to proceed. After many failed attempts, all of sudden the arc of St. Louis caught my attention. The arc is considered as a form of the vertical-horizontal illusion; but it is not quite the same as the standard vertical-horizontal illusion, in which a vertical line sitting on the middle of a horizontal line. If we could straighten the arc and connect the peak of the arc and two ends of the base, we would get a triangle as shown below. We can all agree that the height of the triangle on the left below is longer than its width no matter how you rotate it and from which direction you look at it. This triangle with unequal sides tells us that when we look at the vertical sitting on the horizontal line with equal length, we are not actually looking at and comparing two equal lines but a triangle with sides of different lengths. 

 


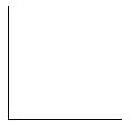
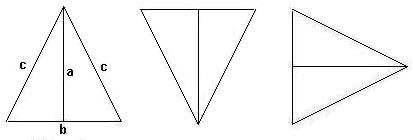
    The above triangle is an isosceles triangle, which has two equal length sides (two c lines) and two equal angles (both at the base). Thus, the c sides are longer than the b side of the triangle. This fact might be the contributing factor for the illusion. If this is the case, all we need to do is to draw an equilateral triangle, which has equal length on all three sides, and draw a vertical line in the middle as the a line in the above figure. 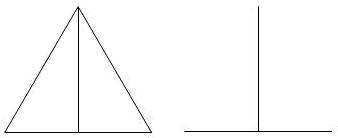If the illusion is caused by the isosceles triangle itself, the vertical line and the horizontal line should look the same length after the two side lines are taken off from the equilateral triangle. However, the figures below show that the vertical line in the equilateral triangle still looks longer than its horizontal line. This means that the illusion is not caused simply by the shape of the triangle. There is definitely something more to it.


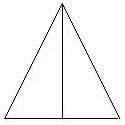
    Since the exercise of the equilateral triangle shows us that the shape of a triangle is not the decisive factor causing the illusion, there must be other force at work. Now we are left with one possibility that the illusion happens because one of the two lines is influenced by more physical force than the other. The vertical line is probably the one that is subjected to more physical force because it appears longer than the horizontal line. Since the two lines are the same length and hence have the same physical force, the extra physical force must stem from somewhere else and exert an influence on the vertical line and make it look longer. Now the task is to find this extra physical force.
    The two c lines in the isosceles triangle above are longer than b line. If we assume that the two longer c lines are somehow influencing the vertical line, making it look longer than the horizontal line, then we can hypothesize that after we know how much longer c lines are than b line, we will know how much a line appears to be longer than b line. Now let's calculate and find out. When b line is 5 cm and the length of c line is 5.59cm, obtained by the formula a2 + b2 = c2, we get:
c - b = 5.59cm - 5cm = 0.59cm.

  From this result, we know that c line is 11.8% longer than b line after the calculations:

0.59cm ÷ 5cm = 0.118cm × 100% = 11.8%.
    Because there are two c lines, as a consequence we should double the physical force that influences the vertical line: 11.8% × 2 = 23.6%. Therefore, the vertical line in the vertical-horizontal illusion looks 23.6% longer than the horizontal line even though they are identical in length. If the c lines are the actual force that affects our perception and causes the illusion, as hypothesized, then the vertical line and the horizontal line should look the same in length when the vertical line is shortened by 23.6%. 

          

    To most observers the vertical lines and horizontal lines in the above figure seem to be the same length, at least very similar. In the above figure, the vertical line is 23.6% shorter than the horizontal line. Therefore, the hypothesis that the longer sides of the isosceles triangle, even though they are invisible in the actual vertical-horizontal illusion, exert some kind of physical force on the vertical line has been confirmed. As to how the two side lines (c lines) in the isosceles triangle influence the vertical line, I don't want to pretend that I have already known the exact answer. As a matter of fact, this is quite baffling to me. What I can do is to guess what happens in our brain or what is the perceptual process.  For the vertical-horizontal illusion, what we see is actually on the retina. But, the triangle, as shown below, is not on our retina. The triangle is something that we don't know for sure whether it exists or not. It is a hypothetical object. If it exists, it must be an entity in the visual cortex, not on the retina. Let's assume that the triangle below is formed in our visual cortex when we look at the standard vertical-horizontal illusion.  Now, we need to know how this triangle, especially the two side lines, can make the vertical line look much longer than the horizontal line as the two lines have the same length.

We can look at the triangle on the left as a mountain. Mountains are made up of earth and rock materials. The outermost layer of the Earth or the Earth's crust is composed of six plates. When two plates move or collide each other, vast land areas are uplifted, resulting in the formation of mountains. There are five major types of mountains; but fold mountains are the most common type of mountains. Examples of fold mountains are the Himalayas (Asia), the Alps (Europe). They are formed due to collision of two plates, causing folding of the Earth's crust. Now, we can imagine that the two side lines are the plates, which meet with each other at the peak of the triangle,  or the peak of the mountain if you like to think this way, and collide each other there. Each side has a force 11.8% more than the vertical line. The collision of these two forces results in the peak being uplifted 23.6% higher. Thus, when we look at the vertical-horizontal illusion, we are looking at a longer vertical line which has been pushed up by two side lines invisible on our retina.  Whether this perceptual process has happened in our brain is unknown. However, we know that it is possible due to its predictive power. I have predicted that the perceived longer portion of the vertical line is due to addition of the extra lengths from two side lines ( c lines in the triangle), and that the vertical line and horizontal line will look the same if the addition of the extra lengths from two side lines is removed from the vertical line. The result, as you can see, is consistent with this prediction. Therefore, it is not over my head to claim that my explanation is superior to the other existing explanations simply because of its predictive power, if not its convincing sensibility. The folding of the Earth's crust is only an imaginary force to explain the height illusions. However, I believe that there exists a force, which is beyond our subjective understanding and manipulation,  that contributes to the longer looking of the vertical line in the height illusions. There are many forces in the universe that we cannot see with our naked eyes, such as gravitational force, electrical force. We know their existence and function based on their effects. Thus, I postulate that the height illusions are caused by an invisible force rather than perceptual errors or perceptual manipulation since our understanding of the perceptual error cannot correct the illusions at all. The force or power that makes the vertical line look longer is objective and beyond our perceptual control, just like the gravitational for or other natural forces which are not subject to our volition.

 I don't blame you if you want to leave the website at this point because you think what I am suggesting is far-fetched and senseless. However,  I urge you to have some patience and stay a little bit longer. My explanation of the vertical-horizontal illusion may be unsatisfactory, but it is a stepping stone for a more complicated and more important illusion, the Müller-Lyer illusion. The similar explanation for the Müller-Lyer illusion has much more predictive power, which can actually predict all those line illusions caused by crossing lines or curves. The approach I have taken to explain the size illusions is to assume that the force or whatever the influence exists independently of our brain; hence it is out of the control of our brain, which is pretty much like the gravitational force. When we fall out of an airplane in the sky, we will fall to the center of the Earth, following the law of gravitation. There is nothing we can do about it; it is beyond our control. Similarly, I believe that the visual illusions are not something that is created or constructed by our brain based on our experience and erroneous interpretations as believed by the conventional wisdom. I believe that the illusions are caused by a force, just like the gravitational force or the electromagnetic force in the nature, which is real and tangible, and independent of our brain and its processing mechanism (if there is any). Although the vertical-horizontal illusion is the simplest of them all, sometimes the simpler things are harder to understand and explain. I find that the more complicated an illusion is, the more satisfactory my explanation turns out to be. For instance, I am most pleased with my explanation of the moon illusion; and the moon illusion is the most complicated illusion among all the size illusions. On the other hand, the explanation for the vertical-horizontal illusion can be backed up by the predictive power of the similar explanations for all the other illusions.

    Some things happen not because of sure, unbreakable laws, but for reasons that we cannot explain. So we just have to go along with what we observe. When we see something happen again and again and again, it is probable that it will continue to happen. It is important to know the true causes of why things happen.  However, most of time we simply cannot determine what the causes are, and what we can actually strive for is to find out the regularity of happening. It is up to you to decide whether I have found the true causes of the size illusions because I am not sure myself. Nevertheless,  nobody should deny that I have discovered the regularities of these major size illusions.


TOP
 

References

Coren, S. & Girgus, J.S. (1978). Seeing is Deceiving: The Psychology of Visual Illusions. New Jersey: Lawrence Erlbaum Associates, Publishers.

Gregory R. L. (1997). Eye and brain: The psychology of seeing (5th ed.). Princeton University Press.

Michaels, C. F., & Carello, C. (1981). Direct perception. Englewood Cliffs, New Jersey: Prentice-Hall, Inc.

Turvey, M. T. (1996). Dynamic touch. American Psychologist, 51, 1134-1152.

Vecera, S. P., Vogel, E. K. & Woodman, G. F. (2002). Lower region: A new cue for figure-ground assignment. Journal of Experimental Psychology: General, 131(2), 194-205.


Related Information on the Web:

http://www.opticalillusion.net/optical-illusions/the-verticalhorizontal-illusion/
http://univ-paris5.academia.edu/mariedemontalembert/Papers/335442/The_vertical-horizontal_illusion_in_hemi-spatial_neglect
http://www.alma.edu/departments/psychology/sp2006/vh/vh.htm
http://books.google.ca/books?id=cs-LSHzKZF4C&pg=PA96&lpg=PA96&dq=vertical-horizontal+illusion&source=bl&ots=PgokYLORRE&sig=RNP6lhTYglH-w5XkEKxOSj3A6lU&hl=en&ei=x7fdTIzJOpTAsAOw_fyFCw&sa=X&oi=book_result&ct=result&resnum=4&ved=0CCcQ6AEwAzgK#




<< Previous    Home    Next >>