Appendix B
Fibonacci Numbers and the Golden Ratio
By Grant Ocean
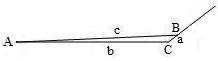
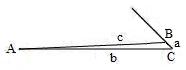
For the Müller-Lyer illusion as discussed in the previous article, I have found the length of the side a in the triangles shown below is always approximately 5% of the length of the side b. The length of the side a in the triangle is obtained when the length of the side c is 103.75% of the side b with outward wings at 135°
angle of ∠C (as shown in the diagram on the left below). Or it is obtained when the length of the side c is 96.25% of the side b with outward wings at 45°
angle of ∠C (as shown in the diagram on the right below). In this article, I am going to investigate why the length of the side a is always approximately 5% of the length of the side b. Is it an irregular and meaningless number or does it demonstrate the regularity in nature?
I hypothesized that this five
percent number is the result of regularities in nature and it is probably a ratio consistent with other regularities
found in nature. This line of thinking prompted me to look for a
meaningful ratio existing in mathematics and nature. What I have found
is the golden ratio.
In mathematics and the arts, two
quantities are in the golden ratio if the ratio between the sum of
those quantities and the larger one is the same as the ratio between
the larger one and the smaller as shown in the diagram below, expressed
algebraically: (a + b) / a = a / b = φ
The golden ratio is an
irrational mathematical constant, approximately 1.61803398875. This
ratio is related to the Fibonacci numbers in which each number is the
sum of the two preceding numbers: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,
144, 233, 377, 610, 987, 1597, 2584, 4181, .... The golden ratio can be obtained by dividing each of the Fibonacci numbers in the sequence by the previous number, to yield the
series:
∞ (infinity), 1, 2, 1.5,
1.6667, 1.6000, 1.6250, 1.6154, 1.6190, 1.6176...
Gradually each
subsequent quotient approaches,
ever closer, the number: 1.61803398875... which is the accurate number
for the golden ratio. We also have to distinguish between two forms:
φ =
1.61803398875... and Φ = 0.61803398875...
where φ is the result of dividing each Fibonacci number by the previous number and Φ is the result of dividing each Fibonacci number by the following number. Both of these numbers are
considered by different authors as the Golden Ratio (although some select one,
some the other). Fortunately, there is
no real problem with this variation since one can quickly discover
that:
1 / φ = 1 /
1.61803398875... = 0.61803398875... =
Φ
This relationship is
accurate to however many decimal places one cares to carry it.
It is quite amazing that the Fibonacci number patterns occur so frequently
in nature ( flowers, shells, plants, leaves, to name a few) that this
phenomenon appears to be one of the principal "laws of nature". Fibonacci
sequences appear in biological settings, in two consecutive Fibonacci numbers,
such as branching in trees, arrangement of leaves on a stem, the fruitlets of a
pineapple, the flowering of artichoke, an uncurling fern and the arrangement of
a pine cone. In addition, numerous claims of the Fibonacci numbers or golden
ratios in nature are found in popular sources, e.g. relating to the breeding
of rabbits, the spirals of shells, and the curve of waves. The Fibonacci numbers or golden
ratios
are also found in the family tree of honeybees, etc. Humans have caught on to this fad-setting trend by composing the musical scale,
where 1 piano has 1 keyboard with black keys arranged in groups of 2 and 3,
consisting of 5 black keys (sharps and flats) and 8 white keys (whole tones) for
a 13 note chromatic musical octave. Musically, we have thus accounted for seven consecutive Fibonacci
numbers. And
from the viewpoint of Nature, this form of music becomes harmonious
with our physical, emotional, mental, and undoubtedly spiritual bodies.
(There are countless articles on the Fibonacci numbers and golden
ratio. If you are interested in the topic, click on the links listed at
the bottom.) In brief, the phenomenon of the Fibonacci numbers can be
summarized in the words of Stan Grist:
The Fibonacci numbers are Nature's numbering system. They appear
everywhere in Nature, from the leaf arrangement in plants, to the pattern of the
florets of a flower, the bracts of a pinecone, or the scales of a pineapple. The
Fibonacci numbers are therefore applicable to the growth of every living thing,
including a single cell, a grain of wheat, a hive of bees, and even all of
mankind.
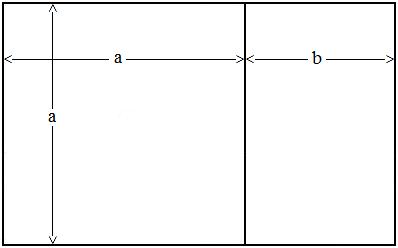
The diagram below
shows a golden rectangle (roughly). The large rectangle is divided into
a square and a smaller rectangle. In a golden rectangle, the smaller
rectangle is the same shape as the larger rectangle; in other words,
their sides are proportional. In further words, the two rectangles are
similar. This can be used as the definition of a golden rectangle. The
proportions give us: (a + b) / a = a / b = φ, which is the
equation for the golden ratio. And then a golden rectangle becomes any
rectangle that exhibits this golden ratio. When the longer side of the
large rectangle is divided by the longer side of the smaller rectangle,
we get φ, and in reverse we get Φ. Similarly, when the shorter side of the large rectangle is divided by the shorter
side of the smaller rectangle, we get φ, and in reverse we get Φ.

The smaller
rectangle can also be divided into a similar square and a even smaller
rectangle, and the process can keep on going. The sides of all these
rectangles as shown in the diagram above are proportional. The
relationship between each rectangle and its next rectangle is a golden
ratio or proportion.
I have come up with a hypothesis based on the golden rectangles as
shown in the diagram above. I have separated seven rectangles as shown
in the diagram below from the above diagram.
Each smaller rectangle is divided from the previous larger rectangle.
My hypothesis is that one of the smaller rectangles has a proportion of
the largest rectangle close to 5%, which is similar to the proportion between the a side and b side in the Müller-Lyer illusion.
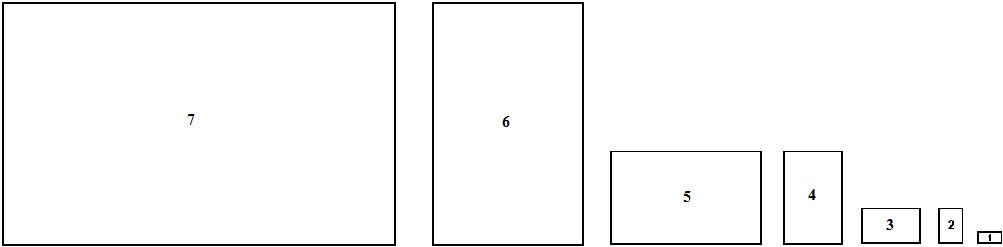
What I have found is that the sides of the number one rectangle in the diagram above,
the smallest, are
approximately 5% of the sides of the number seven rectangle, the
largest in the diagram above. We can also obtain the results from the
Fibonacci numbers.
If any number in the Fibonacci numbers represents the smallest
rectangle and the seventh number afterwords represents the largest
rectangle, as shown inthe figure below,
then we can attain
the proportion between the either side of the smallest rectangle and
the largest rectangle by dividing a Fibonacci number by its seven
subsequent number. For example,
1 ÷ 21 ≈ 0.047619
2 ÷ 34 ≈ 0.058824
3 ÷ 55 ≈ 0.054545
As you can see, the results are
not the same. However, the larger Fibonacci numbers will reach a stable
result. For example, when the 42
nd Fibonacci number is divided by the 48
th Fibonacci number,
we get
267,914,296 ÷ 4,807,526,976 ≈ 0.055728090000841
When the 43
rd Fibonacci number is divided by the 49
th Fibonacci number, we get
433,494,437 ÷ 7,778,742,049 ≈ 0.055728090000841.
This means that as the Fibonacci
numbers are getting large enough, any number is about 5.5728% of its
next seventh number. Or we can say that the either side of the smallest
rectangle is about 5.5728% of that of the largest rectangle in the
diagram above.



Now it is the time to have a close look at the proportion between the
a side and b side in the diagrams below. As I have said before, the length of the a side is approximately 5% of that of the b
side. But I did not get the accurate value for the proportion. For the
purpose of confirming the hypothesis, we need to get an accurate value
for the proportion between the sides a and b. I think that it is relatively easier to find the exact degree for ∠
A than to measure the side a. Then we can calculate the length of the side a by means of the equation: a2 = b2 + c2 -
2bc Cos A.
The value I have got for ∠
A
is slightly less than 2.5°. Since I do not have the precise
measurement, I am going to calculate the proportions between the sides a and b for 2.3°, 2.4°, 2.5° respectively.
First, when
∠
C = 45
°, we have the following results: the side
a is 5.4321% of the side
b when ∠
A = 2.3
°; 5.5574% when ∠
A = 2.4
°; and 5.6852% when ∠
A = 2.5
°. And when
∠
C = 135
°, we have the following results: the side
a is 5.5422% of the side
b when ∠
A = 2.3
°; 5.6745% when ∠
A = 2.4
°; and 5.8094% when ∠
A = 2.5
°.
The ratios of the side a and side b
(see the diagrams above) are very close to the ratio of a Fibonacci
number and its seventh subsequent number, especially the ratio when the
angle A is 2.4 degrees. However, we have not obtained the exact
match between the ratios. Since the golden ratio is an irrational
number, we should not expect to find any exact matches. For instance, the side a should have the same length and hence the same ratio when ∠C = 135° , ∠C = 45° and ∠A is a certain degree. As we see clearly above, the ratios are different. As a result, I can claim that my hypothesis is by and large confirmed.
The golden ratio is only applied
to the proportions between the Fibonacci numbers beyond the adjacent
numbers.
Nobody would accept that the proportion between the Fibonacci numbers
with six numbers in between can be called the golden ratio. Nevertheless, I hypothesized that the ratio of the sides a and b in the triangle which I believe is the cause of the Müller-Lyer illusion
has a close match of the ratio of two Fibonacci numbers. The
measurements and calculations have basically confirmed the hypothesis.
Whether the close match we find here is a fluke or meaningful
regularity in nature is something that requires further investigation.
As far as the hypothesis is concerned, at least it is not disproved. Thus, it provides an additional evidence to support the idea that the invisible c line might be the influencing force for the Müller-Lyer illusion.
TOP
Related Information on the Web:
http://en.wikipedia.org/wiki/Fibonacci_number
http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibnat.html
http://library.thinkquest.org/27890/mainIndex.html
http://www.mathsisfun.com/numbers/golden-ratio.html
http://www.freemasonry.bcy.ca/symbolism/golden_ratio/index.html
http://library.thinkquest.org/C005449/